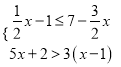题目内容
【题目】等边三角形ABC的边长为6,在AC,BC边上各取一点E、F,连接AF,BE相交于点P,若AE=CF,则∠APB=______.

【答案】120°
【解析】
由已知条件先证△ABE≌△CAF,由此可得∠ABE=∠CAF,从而可得∠BPF=∠ABE+∠BAF=∠CAF+∠BAF=∠BAC=60°,由此即可得出∠APB=180°-60°=120°.
∵△ABC是等边三角形,
∴∠BAC=∠ABC=∠BCA=60°,AB=CA,
∵在△ABE和△CAF中: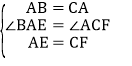 ,
,
∴△ABE≌△CAF(SAS),
∴∠ABE=∠CAF,
∴∠BPF=∠ABE+∠BAP=∠CAF+∠BAP=∠BAC=60°,
∴∠APB=180°-60°=120°.
故答案为:120°.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
【题目】为了美化校园环境,争创绿色学校,某县教育局委托园林公司对A,B两校进行校园绿化,已知A校有如图![]() 的阴影部分空地需铺设草坪,B校有如图
的阴影部分空地需铺设草坪,B校有如图![]() 的阴影部分空地需铺设草坪,在甲、乙两地分别有同种草皮3500米
的阴影部分空地需铺设草坪,在甲、乙两地分别有同种草皮3500米![]() 和2500米
和2500米![]() 出售,且售价一样,若园林公司向甲、乙两地购买草皮,其路程和运费单价表如下:
出售,且售价一样,若园林公司向甲、乙两地购买草皮,其路程和运费单价表如下:
路程、运费单价表
A校 | B校 | |||
路程 | 运费单价 | 路程 | 运费单价 | |
甲地 | 20 |
| 10 |
|
乙地 | 15 |
| 20 | |
![]() 注:运费单价表示每平方米草皮运送1千米所需的人民币
注:运费单价表示每平方米草皮运送1千米所需的人民币![]()

求:![]() 分别求出图1、图2的阴影部分面积;
分别求出图1、图2的阴影部分面积;
![]() 若园林公司将甲地
若园林公司将甲地![]() 的草皮全部运往A校,请你求出园林公司运送草皮去A、B两校的总运费;
的草皮全部运往A校,请你求出园林公司运送草皮去A、B两校的总运费;
![]() 请你给出一种运送方案,使得园林公司支付出送草皮的总运费不超过15000元.
请你给出一种运送方案,使得园林公司支付出送草皮的总运费不超过15000元.