题目内容
如图,Rt△OAB中,∠OAB=90°,O为坐标原点,边OA在x轴上,OA=AB=1个单位长度.把Rt△OAB沿x轴正方向平移1个单位长度后得△![]() .
.
(1)求以A为顶点,且经过点![]() 的抛物线的解析式;
的抛物线的解析式;
(2)若(1)中的抛物线与OB交于点C,与y轴交于点D,求点D、C的坐标.
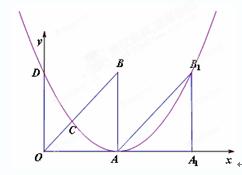
解:(1)由题意,得A (1,0),![]() (2,0),
(2,0),![]() (2,1).设以A为顶点的抛物线的解析式为
(2,1).设以A为顶点的抛物线的解析式为![]() ∵ 此抛物线过点
∵ 此抛物线过点![]() (2,1),∴ 1=a (2-1)2.∴ a=1.
(2,1),∴ 1=a (2-1)2.∴ a=1.
∴ 抛物线的解析式为y=(x-1)2.
:(2)方法1:∵ 当x=0时,y=(0-1)2=1.∴ D点坐标为 (0,1).
由题意可知OB在第一象限的角平分线上,故可设C (m,m),代入y=(x-1)2,得m=(m-1)2, 解得m1=![]() <1,m2=
<1,m2=![]() >1(舍去).∴
>1(舍去).∴ ![]() .
.
方法2:令x=0,y=(0-1)2=1,∴D点坐标为(0,1).
∵直线OB在第一、三象限的角平分线上,∴直线OB的解析式为:y=x
根据题意得,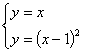 解得
解得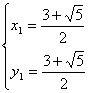
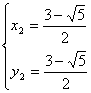
∵x1=![]() >1(舍去),所以点C坐标为(
>1(舍去),所以点C坐标为(![]() ,
,![]() ).
).

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
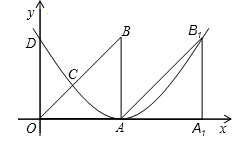 方向平移1个单位长度后得△AA1B1.
方向平移1个单位长度后得△AA1B1. (2013•桥东区二模)如图在Rt△OAB中,∠OAB=90°,OA=AB=6.
(2013•桥东区二模)如图在Rt△OAB中,∠OAB=90°,OA=AB=6.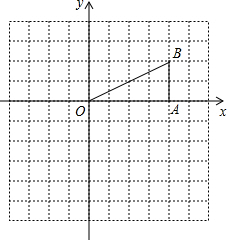 如图,Rt△OAB中,∠OAB=90°,B(4,2).
如图,Rt△OAB中,∠OAB=90°,B(4,2).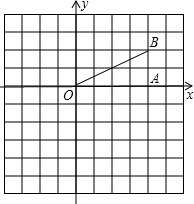 (1)如图,Rt△OAB中,∠OAB=90°,B(4,2),△OAB向下平移3个单位后得△O1A1B1,画出△O1A1B1;
(1)如图,Rt△OAB中,∠OAB=90°,B(4,2),△OAB向下平移3个单位后得△O1A1B1,画出△O1A1B1;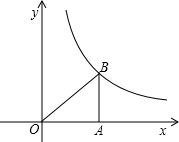 如图,Rt△OAB中,∠OAB=90°,OA=AB,且△OAB的面积为9,函数
如图,Rt△OAB中,∠OAB=90°,OA=AB,且△OAB的面积为9,函数