题目内容
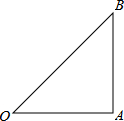 (2013•桥东区二模)如图在Rt△OAB中,∠OAB=90°,OA=AB=6.
(2013•桥东区二模)如图在Rt△OAB中,∠OAB=90°,OA=AB=6.(1)请你画出将△OAB绕点O沿逆时针方向旋转90°,得到的△OA1B1;
(2)线段OA1的长度是
6
6
,∠AOB1的度数是135°
135°
;(3)连接AA1,求证:四边形OAA1B1是平行四边形.
分析:(1)根据旋转中心为点O,旋转方向逆时针,旋转角度90°得到点A、B的对应点A1,B1,顺次连接O、A1、B1即可得到△OA1B1;
(2)根据旋转的性质知,旋转图形的对应边、对应角都相等;
(3)根据平行四边形的判定定理“对边平行且相等的四边形是平行四边形”进行证明.
(2)根据旋转的性质知,旋转图形的对应边、对应角都相等;
(3)根据平行四边形的判定定理“对边平行且相等的四边形是平行四边形”进行证明.
解答: (1)解:△OA1B1如图所示.
(1)解:△OA1B1如图所示.
(2)解:根据旋转的性质知,OA1=OA=6.
∵将△OAB绕点O沿逆时针方向旋转90°,得到的△OA1B1,
∴∠BOB1=90°.
∵在Rt△OAB中,∠OAB=90°,OA=AB=6,
∴∠BOA=∠OBA=45°,
∴∠AOB1=∠BOB1+∠BOA=90°+45°=135°,即∠AOB1的度数是135°.
故答案是:6,135°;
(3)证明:根据旋转的性质知,△OA1B1≌△OAB,
则∠OA1B1=∠OAB=90°,A1B1=AB,
∵将△OAB绕点O沿逆时针方向旋转90°,得到的△OA1B1,
∴∠A1OA=90°,
∴∠OA1B1=∠A1OA,
∴A1B1∥OA.
又∵OA=AB,
∴A1B1=OA,
∴四边形OAA1B1是平行四边形.
 (1)解:△OA1B1如图所示.
(1)解:△OA1B1如图所示.(2)解:根据旋转的性质知,OA1=OA=6.
∵将△OAB绕点O沿逆时针方向旋转90°,得到的△OA1B1,
∴∠BOB1=90°.
∵在Rt△OAB中,∠OAB=90°,OA=AB=6,
∴∠BOA=∠OBA=45°,
∴∠AOB1=∠BOB1+∠BOA=90°+45°=135°,即∠AOB1的度数是135°.
故答案是:6,135°;
(3)证明:根据旋转的性质知,△OA1B1≌△OAB,
则∠OA1B1=∠OAB=90°,A1B1=AB,
∵将△OAB绕点O沿逆时针方向旋转90°,得到的△OA1B1,
∴∠A1OA=90°,
∴∠OA1B1=∠A1OA,
∴A1B1∥OA.
又∵OA=AB,
∴A1B1=OA,
∴四边形OAA1B1是平行四边形.
点评:本题考查了作图--旋转变换,平行四边形的判定.旋转作图有自己独特的特点,决定图形位置的因素较多,旋转角度、旋转方向、旋转中心不同,位置就不同,但得到的图形全等.

练习册系列答案
相关题目
 (2013•桥东区二模)如图,Rt△ABC在平面直角坐标系中,BC在x轴上,B(-1,0)、A(0,2),AC⊥AB.
(2013•桥东区二模)如图,Rt△ABC在平面直角坐标系中,BC在x轴上,B(-1,0)、A(0,2),AC⊥AB.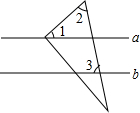 (2013•桥东区二模)如图,a∥b,将三角尺的直角顶点放在直线a上,∠1=50°,∠2=60°,则∠3=
(2013•桥东区二模)如图,a∥b,将三角尺的直角顶点放在直线a上,∠1=50°,∠2=60°,则∠3=