题目内容
如图,Rt△OAB中,∠OAB=90°,O为坐标原点,边OA在x轴上,OA=AB=1个单位长度,把Rt△OAB沿x轴正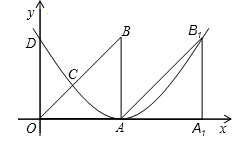 方向平移1个单位长度后得△AA1B1.
方向平移1个单位长度后得△AA1B1.(1)求以A为顶点,且经过点B1的抛物线的解析式;
(2)若(1)中的抛物线与OB交于点C,与y轴交于点D,求点D、C的坐标.
分析:(1)先设抛物线的解析式为y=a(x-1)2,再将B1点坐标代入抛物线的解析式即可得出答案;
(2)令x=0即可求出D点坐标,再设出C点坐标C(m,m),代入抛物线解析式解方程即可求得C点坐标.
(2)令x=0即可求出D点坐标,再设出C点坐标C(m,m),代入抛物线解析式解方程即可求得C点坐标.
解答:解:(1)由题意可知,A(1,0),A1(2,0),B1(2,1),
设以A为顶点的抛物线的解析式为y=a(x-1)2;
∵此抛物线过点B1(2,1),
∴1=a(2-1)2,
∴a=1,
∴抛物线的解析式为y=(x-1)2;
(2)∵当x=0时,y=(0-1)2=1,
∴D点坐标为(0,1),
由题意得OB在第一象限的角平分线上,
故可设C(m,m),
代入y=(x-1)2;得m=(m-1)2;
解得m1=
<1,m2=
>1(舍去).
故C点坐标为(
,
).
设以A为顶点的抛物线的解析式为y=a(x-1)2;
∵此抛物线过点B1(2,1),
∴1=a(2-1)2,
∴a=1,
∴抛物线的解析式为y=(x-1)2;
(2)∵当x=0时,y=(0-1)2=1,
∴D点坐标为(0,1),
由题意得OB在第一象限的角平分线上,
故可设C(m,m),
代入y=(x-1)2;得m=(m-1)2;
解得m1=
3-
| ||
| 2 |
3+
| ||
| 2 |
故C点坐标为(
3-
| ||
| 2 |
3-
| ||
| 2 |
点评:本题是二次函数的综合题,其中涉及到的知识点有抛物线的公式的求法,是各地中考的热点和难点,解题时注意数形结合等数学思想的运用,同学们要加强训练,属于中档题.

练习册系列答案
相关题目
 (2013•桥东区二模)如图在Rt△OAB中,∠OAB=90°,OA=AB=6.
(2013•桥东区二模)如图在Rt△OAB中,∠OAB=90°,OA=AB=6.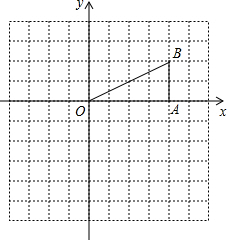 如图,Rt△OAB中,∠OAB=90°,B(4,2).
如图,Rt△OAB中,∠OAB=90°,B(4,2).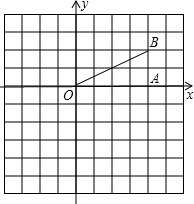 (1)如图,Rt△OAB中,∠OAB=90°,B(4,2),△OAB向下平移3个单位后得△O1A1B1,画出△O1A1B1;
(1)如图,Rt△OAB中,∠OAB=90°,B(4,2),△OAB向下平移3个单位后得△O1A1B1,画出△O1A1B1;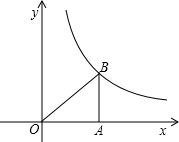 如图,Rt△OAB中,∠OAB=90°,OA=AB,且△OAB的面积为9,函数
如图,Rt△OAB中,∠OAB=90°,OA=AB,且△OAB的面积为9,函数