题目内容
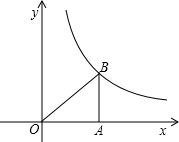 如图,Rt△OAB中,∠OAB=90°,OA=AB,且△OAB的面积为9,函数y=
如图,Rt△OAB中,∠OAB=90°,OA=AB,且△OAB的面积为9,函数y=| k | x |
(1)求点B的坐标;
(2)求反比例函数的解析式.
分析:(1)根据三角形的面积公式得到S△OAB=
OA•AB=9,由于OA=AB,可求得OA=AB=3
,则B(3
,3
);
(2)根据k的几何意义得到k=2S△OAB=18.
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
(2)根据k的几何意义得到k=2S△OAB=18.
解答:解:(1)∵Rt△OAB中,∠OAB=90°,OA=AB,
∴S△OAB=
OA•AB=9,
∴OA=AB=3
,
∴B(3
,3
),
(2)k=2S△OAB=18,所以反比例函数的解析式为y=
.
∴S△OAB=
| 1 |
| 2 |
∴OA=AB=3
| 2 |
∴B(3
| 2 |
| 2 |
(2)k=2S△OAB=18,所以反比例函数的解析式为y=
| 18 |
| x |
点评:本题考查了反比例y=
(k≠0)数k的几何意义:过反比例函数图象上任意一点分别作x轴、y轴的垂线,则垂线与坐标轴所围成的矩形的面积为|k|.
| k |
| x |

练习册系列答案
相关题目
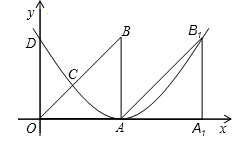 方向平移1个单位长度后得△AA1B1.
方向平移1个单位长度后得△AA1B1. (2013•桥东区二模)如图在Rt△OAB中,∠OAB=90°,OA=AB=6.
(2013•桥东区二模)如图在Rt△OAB中,∠OAB=90°,OA=AB=6.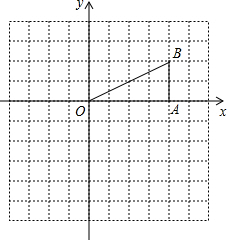 如图,Rt△OAB中,∠OAB=90°,B(4,2).
如图,Rt△OAB中,∠OAB=90°,B(4,2).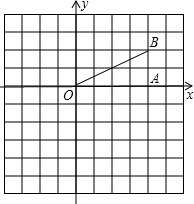 (1)如图,Rt△OAB中,∠OAB=90°,B(4,2),△OAB向下平移3个单位后得△O1A1B1,画出△O1A1B1;
(1)如图,Rt△OAB中,∠OAB=90°,B(4,2),△OAB向下平移3个单位后得△O1A1B1,画出△O1A1B1;