题目内容
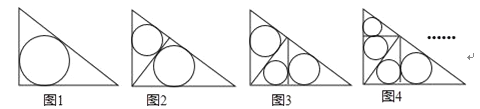
【题目】如图1～4，在直角边分别为3和4的直角三角形中，每多作一条斜边上的高就增加一个三角形的内切圆，依此类推，图10中有10个直角三角形的内切圆，它们的面积分别记为S1，S2，S3，…，S10，则S1+S2+S3+…+S10= ．
【答案】p.
【解析】
试题（1）图1，作辅助线构建正方形OECF，设圆O的半径为r，根据切线长定理表示出AD和BD的长，利用AD+BD=5列方程求出半径
=1（a、b是直角边，c为斜边），运用圆面积公式=πr2求出面积=π；
（2）图2，先求斜边上的高CD的长，再由勾股定理求出AD和BD，利用半径（a、b是直角边，c为斜边）求两个圆的半径分别是
，从而求出两圆的面积和=π；
（3）图3，继续求高DM和CM、BM，利用半径（a、b是直角边，c为斜边）求三个圆的半径分别是
，从而求出三个圆的面积和=π；
综上所述：发现S1+S2+S3+…+S10=π．
练习册系列答案
阅读快车系列答案
相关题目
【题目】某校数学兴趣小组，对函数y＝|x﹣1|+1的图象和性质进行了探究，探究过程如下：
（1）自变量x的取值范围是全体实数，x与y的几组对应值如表：
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 5 | 4 | m | 2 | 1 | 2 | 3 | 4 | 5 | … |
其中m＝ ．
（2）如图，在平面直角坐标系xOy中，描出了上表中各对对应值为坐标的点，根据描出的点，画出该函数的图象：
（3）根据画出的函数图象特征，仿照示例，完成下列表格中的函数变化规律：
序号 | 函数图象特征 | 函数变化规律 |
示例1 | 在直线x＝1的右侧，函数图象呈上升状态 | 当x＞1时，y随x的增大而增大 |
① | 在直线x＝1的左侧，函数图象呈下降状态 |
|
示例2 | 函数图象经过点（﹣3，5） | 当x＝﹣3时，y＝5 |
② | 函数图象的最低点是（1，1） |
|
（4）当2＜y≤4时，x的取值范围为 ．
