题目内容
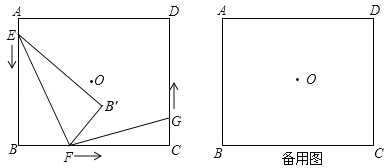
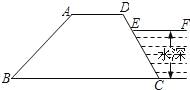
【题目】有一水库大坝的横截面是梯形ABCD，AD∥BC，EF为水库的水面，点E在DC上，某课题小组在老师的带领下想测量水的深度，他们测得背水坡AB的长为12米，迎水坡上DE的长为2米，∠BAD=135°，∠ADC=120°，求水深．（精确到0.1米，
=1.41，
=1.73）
【答案】水深约为6.7米
【解析】
分别过A、D作AM⊥BC于M，DG⊥BC于G．利用AB的长为12，∠BAD=135°可求得梯形的高的长度．这两条高相等，再利用DE长构造一直角三角形，求得DE的垂直距离，进而求得水深．
分别作AM⊥BC于M，DG⊥BC于G．过E作EH⊥DG于H，则四边形AMGD为矩形．
∵AD∥BC，∠BAD=135°，∠ADC=120°．
∴∠B=45°，∠DCG=60°，∠GDC=30°．
在Rt△ABM中，
AM=ABsinB=12×
=6
，
∴DG=6．
在Rt△DHE中，
DH=DEcos∠EDH=2×
=
，
∴HG=DG-DH=6-≈6×1.41-1.73≈6.7．
答：水深约为6.7米．
练习册系列答案
相关题目
