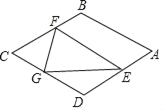
题目内容
【题目】以四边形![]() 的边
的边![]() 、
、![]() 、
、![]() 、
、![]() 为斜边分别向外侧作等腰直角三角形,直角顶点分别为
为斜边分别向外侧作等腰直角三角形,直角顶点分别为![]() 、
、![]() 、
、![]() 、
、![]() ,顺次连结这四个点,得四边形
,顺次连结这四个点,得四边形![]() .
.
(1)如图1,当四边形![]() 为矩形时,请判断四边形
为矩形时,请判断四边形![]() 的形状(不要求证明).
的形状(不要求证明).
(2)如图2,当四边形![]() 为一般平行四边形时,设
为一般平行四边形时,设![]()
①试用含![]() 的代数式表示
的代数式表示![]() ,写出解答过程;
,写出解答过程;
②求证:![]() ,并判断四边形
,并判断四边形![]() 是什么四边形?请说明理由.
是什么四边形?请说明理由.
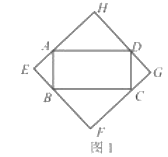
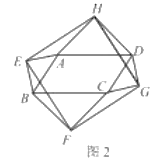
【答案】(1)四边形![]() 是正方形;
是正方形;
(2)①![]() =90°+
=90°+![]() ,②HE=HG证明过程见详解;
,②HE=HG证明过程见详解;
四边形![]() 是正方形,理由见详解.
是正方形,理由见详解.
【解析】
(1)根据等腰直角三角形的性质得到∠E=∠F=∠G=∠H=90°,求出四边形是矩形,根据勾股定理求出AH=HD=![]() AD,DG=GC=
AD,DG=GC=![]() DC ,BF=CF=
DC ,BF=CF=![]() BC,EA=EB=
BC,EA=EB=![]() AB,推出EF=FG=GH=EH,根据正方形的判定推出四边形EFGH是正方形即可;
AB,推出EF=FG=GH=EH,根据正方形的判定推出四边形EFGH是正方形即可;
(2)①根据平行四边形的性质得出,∠BAD=180°-![]() ,根据△HAD和△EAB是等腰直角三角形,得到∠HAD=∠EAB=45°,求出∠HAE即可;
,根据△HAD和△EAB是等腰直角三角形,得到∠HAD=∠EAB=45°,求出∠HAE即可;
②根据△AEB和△DGC是等腰直角三角形,得出AE=![]() AB,DG=
AB,DG=![]() CD,平行四边形的性质得出AB=CD,求出∠HDG=90°+
CD,平行四边形的性质得出AB=CD,求出∠HDG=90°+![]() =∠HAE,根据SAS证△HAE≌△HDG,根据全等三角形的性质即可得出HE=HG;同理可得GH=GF,FG=FE,推出GH=GF=EF=HE,得出菱形EFGH,根据∠AHD=90°得∠EHG=90°,即可推出结论.
=∠HAE,根据SAS证△HAE≌△HDG,根据全等三角形的性质即可得出HE=HG;同理可得GH=GF,FG=FE,推出GH=GF=EF=HE,得出菱形EFGH,根据∠AHD=90°得∠EHG=90°,即可推出结论.
解:(1)∵以矩形![]() 的边
的边![]() 、
、![]() 、
、![]() 、
、![]() 为斜边分别向外侧作等腰直角三角形,
为斜边分别向外侧作等腰直角三角形,
∴∠E=∠F=∠G=∠H=90°,∠HAD=∠EAB=45°,∠BAD=90°,
∴∠EAH=180°,即E、A、H三点在一条直线上,
同理可知:E、B、F三点共线,F、C、G三点共线,G、D、H三点共线,
∴AH=HD=![]() AD,DG=GC=
AD,DG=GC=![]() DC ,BF=CF=
DC ,BF=CF=![]() BC,EA=EB=
BC,EA=EB=![]() AB,
AB,
∴EF=FG=GH=EH,
∴四边形EFGH是正方形.
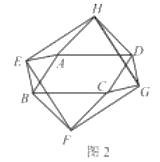
(2)①∠HAE=90°+![]()
解:在平行四边形ABCD中
AB//CD,
∴∠BAD=180°-∠ADC=180°-![]()
∵△HAD和△EAB是等腰直角三角形,
∴∠HAD=∠EAB=45°,
∴∠HAE=360°-∠HAD-∠EAB-∠BAD=360°-45°-45°-(180°-![]() )=90°+
)=90°+![]()
故用含![]() 的代数式表示∠HAE是90°+
的代数式表示∠HAE是90°+![]()
,
②证明:∵△AEB和△DGC是等腰直角三角形,
∴AE=![]() AB,DG=
AB,DG=![]() DC
DC
∵平行四边形ABCD中,AB=CD,
∴AE=DG,
∵△AHD和△DGC是等腰直角三角形,
∴∠HDA=∠CDG=45°,
∴∠HDG=∠HDA+∠ADC+∠CDG=90°+![]() =∠HAE
=∠HAE
∵△AHD是等腰直角三角形
∴HA=HD
∴△HAE≌△HDG
∴HE=HG.
答:四边形EFGH是正方形
理由是:
由以上同理可得:
GH=GF,FG=FE,
∵HE=HG,
∴GH=GF=EF=HE,
∴四边形EFGH是菱形,
∵△HAE≌△HDG,
∴∠DHG=∠AHE,
∵∠AHD=∠AHG+∠DHG=90°
∴∠EHG=∠AHG+∠AHE=90°
∴四边形EFGH是正方形.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案【题目】某商店一周内甲、乙两种计算器每天的销售量如下(单位:个):
类别/星期 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 平均数 |
甲 |
|
|
|
|
|
|
| |
乙 |
|
|
|
|
|
|
|
|
(1)将表格填写完整.
(2)求甲种计算器本周销售量的方差.
(3)已知乙种计算器本周销售量的方差为![]() ,本周哪种计算器的销售量比较稳定?说明理由.
,本周哪种计算器的销售量比较稳定?说明理由.