题目内容
【题目】四位同学在研究函数![]() (
(![]() 是常数)时,甲发现当
是常数)时,甲发现当![]() 时,函数有最小值;乙发现
时,函数有最小值;乙发现![]() 是方程
是方程![]() 的一个根;丙发现函数的最小值为3;丁发现当
的一个根;丙发现函数的最小值为3;丁发现当![]() 时,
时,![]() ,已知这四位同学中只有一位发现的结论是错误的,则该同学是( )
,已知这四位同学中只有一位发现的结论是错误的,则该同学是( )
A.甲B.乙C.丙D.丁
【答案】B
【解析】
利用假设法逐一分析,分别求出二次函数的解析式,再判断与假设是否矛盾即可得出结论.
解:A.假设甲同学的结论错误,则乙、丙、丁的结论都正确
由乙、丁同学的结论可得
![]()
解得:
∴二次函数的解析式为:![]()
∴当x=![]() 时,y的最小值为
时,y的最小值为![]() ,与丙的结论矛盾,故假设不成立,故本选项不符合题意;
,与丙的结论矛盾,故假设不成立,故本选项不符合题意;
B.假设乙同学的结论错误,则甲、丙、丁的结论都正确
由甲、丙的结论可得二次函数解析式为![]()
当x=2时,解得y=4,当x=-1时,y=7≠0
∴此时符合假设条件,故本选项符合题意;
C. 假设丙同学的结论错误,则甲、乙、丁的结论都正确
由甲乙的结论可得
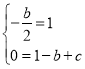
解得:![]()
∴![]()
当x=2时,解得:y=-3,与丁的结论矛盾,故假设不成立,故本选项不符合题意;
D. 假设丁同学的结论错误,则甲、乙、丙的结论都正确
由甲、丙的结论可得二次函数解析式为![]()
当x=-1时,解得y=7≠0,与乙的结论矛盾,故假设不成立,故本选项不符合题意.
故选B.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案
相关题目