题目内容
【题目】阅读下列材料:我们知道![]() 的几何意义是在数轴上数
的几何意义是在数轴上数![]() 对应的点与原点的距离,即
对应的点与原点的距离,即![]() ,也就是说,
,也就是说,![]() 表示在数轴上数
表示在数轴上数![]() 与数
与数![]() 对应点之间的距离.这个结论可以推广为:
对应点之间的距离.这个结论可以推广为:![]() 表示在数轴上数
表示在数轴上数![]() 与
与![]() 对应点之间的距离.
对应点之间的距离.
例![]() 已知
已知![]() ,求
,求![]() 的值.
的值.
解:在数轴上与原点距离为![]() 的点的对应数为
的点的对应数为![]() 和
和![]() ,即
,即![]() 的值为
的值为![]() 和
和![]() .
.
例![]() 已知
已知![]() ,求
,求![]() 的值.
的值.
解:在数轴上与![]() 的距离为
的距离为![]() 点的对应数为
点的对应数为![]() 和
和![]() ,即
,即![]() 的值为
的值为![]() 和
和![]() .
.
仿照阅读材料的解法,解决下列问题:
(1)已知![]() ,求
,求![]() 的值;
的值;
(2)已知![]() ,求
,求![]() 的值;
的值;
(3)若数轴上表示![]() 的点在
的点在![]() 与
与![]() 之间,则
之间,则![]() 的值为_________;
的值为_________;
(4)当![]() 满足_________时,则
满足_________时,则![]() 的值最小,最小值是_________.
的值最小,最小值是_________.
【答案】(1)-3和3.(2)-6和2;(3)6;(4)1≤a≤1
【解析】试题(1)根据绝对值的性质即可求得a值;(2)根据绝对值的性质可得a+2=4或a+2=-4,解方程即可得a的值;(3)由数轴上表示a的点在-4与2之间,可得|a+4|+|a-2|的值为2-|-4|;(4)根据线段上的点与线段两端点的距离的和最小,可得答案.
试题解析:
(1)在数轴上与原点距离为![]() 的点的对应数为
的点的对应数为![]() 和
和![]() ,即
,即![]() 的值为
的值为![]() 和
和![]() .
.
(2)在数轴上与![]() 距离为
距离为![]() 的点的对应数为
的点的对应数为![]() 和
和![]() ,即
,即![]() 的值为
的值为![]() 和
和![]() .
.
(3)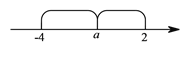
![]()
(4)![]() 取中间一段,
取中间一段,![]() 时,最小值为
时,最小值为![]()

练习册系列答案
相关题目