题目内容
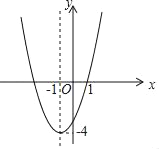
【题目】如图,抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴负半轴交于点
轴负半轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,且
,且![]() .
.
(1)求抛物线的解析式;
(2)点![]() 在
在![]() 轴上,且
轴上,且![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)点![]() 在抛物线上,点
在抛物线上,点![]() 在抛物线的对称轴上,是否存在以点
在抛物线的对称轴上,是否存在以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形?若存在。求出所有符合条件的点
为顶点的四边形是平行四边形?若存在。求出所有符合条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

【答案】(1) 抛物线解析式为![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() ,
,![]() ,
,![]() .
.
【解析】
(1)根据当![]() 时,
时,![]() 可知C(0,-3)根据
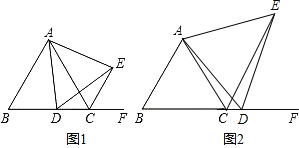
可知C(0,-3)根据![]() ,可知B(-1,0)利用待定系数法求出抛物线的解析式即可.(2)如图:连接AC,作BF⊥AC交AC的延长线于F,根据已知条件得到AF∥x轴,得到F(-1,-3),可知∠BAC=45°,设D(0,m),则OD=|m|根据∠BDO=∠BAC=45°,即可得到结论;(3)设M(a,a2-2a-3),N(1,n),①以AB为边,则AB∥MN,AB=MN,如图:过M作ME⊥对称轴y于E,AF⊥x轴于F,于是得到△ABF≌△NME,证得NE=AF=3,ME=BF=3,得到M(4,5)或(-2,11);②以AB为对角线,BN=AM,BN∥AM,如图3,则N在x轴上,M与C重合,于是得到结论.
,可知B(-1,0)利用待定系数法求出抛物线的解析式即可.(2)如图:连接AC,作BF⊥AC交AC的延长线于F,根据已知条件得到AF∥x轴,得到F(-1,-3),可知∠BAC=45°,设D(0,m),则OD=|m|根据∠BDO=∠BAC=45°,即可得到结论;(3)设M(a,a2-2a-3),N(1,n),①以AB为边,则AB∥MN,AB=MN,如图:过M作ME⊥对称轴y于E,AF⊥x轴于F,于是得到△ABF≌△NME,证得NE=AF=3,ME=BF=3,得到M(4,5)或(-2,11);②以AB为对角线,BN=AM,BN∥AM,如图3,则N在x轴上,M与C重合,于是得到结论.
(1)当![]() 时,
时,![]() ,
,![]() ,
,
![]() ,
,
![]() .
.![]() ,
,![]() ,
,
![]() 抛物线解析式为
抛物线解析式为![]() .
.
(2)连接AC,作BF⊥AC交AC的延长线于F,
∵A(2,-3),C(0,-3),
∴AF∥x轴,
∴F(-1,-3),
∴BF=3,AF=3,
∴∠BAC=45°,
设D(0,m),则OD=|m|,
∵∠BDO=∠BAC,
∴∠BDO=45°,
∴OD=OB=1,
∴|m|=1,
∴m=±1,
∴D1(0,1),D2(0,-1);
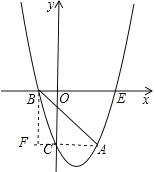
(3)设M(a,a2-2a-3),N(1,n),
①以AB/span>为边,则AB∥MN,AB=MN,过M作ME⊥对称轴y于E,AF⊥x轴于F,
则△ABF≌△NME,
∴NE=AF=3,ME=BF=3,
∴|a-1|=3,
∴a=4或a=-2,
∴M(4,5)或(-2,5);
②以AB为对角线,BN=AM,BN∥AM,如图,
则N在x轴上,M与C重合,
∴M(0,-3),
综上所述,存在以点A,B,M,N为顶点的四边形是平行四边形,M(4,5)或(-2,5)或(0,-3).

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案【题目】某水果超市为了吸引顾客来店购物,设立了一个如图所示的可以自由转动的转盘,开展有奖购物活动.顾客购买商品满200元就能获得一次转动转盘的机会,当转盘停止时,指针落在“一袋苹果”的区域就可以获得“一袋苹果”的奖品;指针落在“一盒樱桃”的区域就可以获得“一盒樱桃”的奖品.下表是该活动的一组统计数据:
转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“一袋苹果”区域的次数m | 68 | 108 | 140 | 355 | 560 | 690 |
落在“一袋苹果”区域的频率 | 0.68 | 0.72 | 0.70 | 0.71 | 0.70 | 0.69 |
下列说法不正确的是( )

A. 当n很大时,估计指针落在“一袋苹果”区域的频率大约是0.70
B. 假如你去转动转盘一次,获得“一袋苹果”的概率大约是0.70
C. 如果转动转盘2000次,指针落在“一盒樱桃”区域的次数大约有600次
D. 转动转盘10次,一定有3次获得“一盒樱桃”