Question

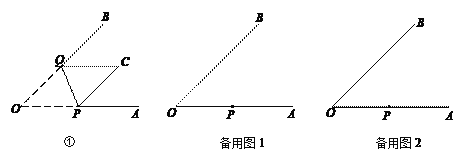
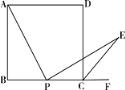
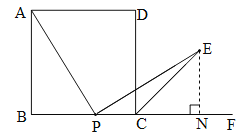
【题目】如图，在正方形ABCD中，P是BC上一动点，（不与B、C重合）① CE平分∠DCF，② AP⊥PE，③ AP=EP．以此三个条件中的两个为条件，另一个为结论，可构成三个命题，即：①② ③，①③ ②，②③ ①．

（1）试判断上述三个命题是否正确（直接作答）；

（2）请选择一个你认为正确的命题给予证明．

Answer 1

【答案】（1）①②③；①③②；②③①上述三个命题均正确；（2）①②③，①③②，②③①证明见解析.

【解析】

（1）三个命题都成立；

（2）在AB边上截取BM=BP，连结MP．通过证明△AMP≌△PCE，可证明①② ③；过E点作EN⊥PF，通过证明△ABP≌△PNE，可证明①③ ②；过E点作EN⊥CF，通过证明△ABP≌△PNE，可证明②③①．

（1）①②③；①③②；②③①上述三个命题均正确；

（2）证明①②③

在AB边上截取BM=BP，连结MP．

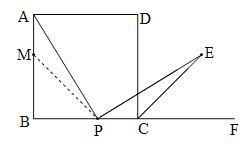
∵BM=BP，∴∠BMP=∠BPM=45°，AM=PC，∴∠AMP=135．

∵ABCD是正方形，CE平分∠DCF，∴∠PCE=135，∴∠AMP=∠PCE．

∵AP⊥PE，∴∠APB+∠EPC=90°．

∵∠BAP+∠APB=90°，∴∠BAP=∠EPC．

在△AMP和△PCE中，∵∠BAP=∠EPC ，AM=PC，∠AMP=∠PCE，∴△AMP≌△PCE，∴PA=PE．

证明①③②

过E点作EN⊥PF．

CE平分∠DCF，∴∠ECN=90°÷2=45°，∴△ECN是等腰直角三角形，∴EN=CN．

∵ABCD是正方形，∴AB=BC．

又∵PA2=AB2+BP2，PE2=PN2+EN2，∴AB2+BP2=PN2+EN2，∴（BP+PC）2+BP2=（PC+CN）2+CN2，∴2BP2+2BPPC=2CN2+2CNPC，∴BP2-CN2+BPPC-CNPC=0，∴（BP+CN）（BP-CN）+PC（BP-CN）=0，∴（BP+CN+PC）（BP-CN）=0，∴BP=CN=EN．

在Rt△ABP和Rt△PNE中，∵AP=PE，BP=EN，∴△ABP≌△PNE，∴∠APB=∠PEN．

∵∠EPC+∠PEN=90°，∴∠APB+∠EPC=90°，∴∠APE=90°，∴PA⊥PE．

证明②③①

过E点作EN⊥CF．

∵EN⊥CF，∴∠EPN+∠PEN=90°．

∵PA⊥PE，∴∠APB+∠EPN=90°，∴∠APB=∠EPN．

在△ABP和△PNE中，∵∠APB=∠EPN ，∠B=∠PNE=90°，AP=PE，∴△ABP≌△PNE，∴BP=EN，AB=PN．

又∵AB=BC，∴BP=EN=CN，∴∠ECN=45，∴CE平分∠DCF．