题目内容
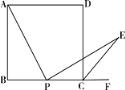
【题目】如图,把矩形![]() 沿
沿![]() 翻折,点
翻折,点![]() 恰好落在
恰好落在![]() 边的
边的![]() 处,若
处,若![]() ,
,![]() ,则
,则![]() 的面积是( )
的面积是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
根据翻折的性质可得出“BF=B′F,∠BFE=∠B′FE,设AE=A′E=x,∠A′B′F=∠B=90°,∠A′=∠A=90°”,根据平行线的性质以及∠EFB=60°即可得出∠B′EF=∠B′FE=60°,进而得出△B′EF为等边三角形,在Rt△A′B′E中,结合特殊角、勾股定理求出B′E的长度,再依据等边三角形的性质以及三角形的面积公式即可得出结论.
解:∵四边形ABCD为矩形,
∴∠B=∠A=90°,AD∥BC.
由翻折的性质可知:
BF=B′F,∠BFE=∠B′FE,设AE=A′E=x,∠A′B′F=∠B=90°,∠A′=∠A=90°.
∵∠EFB=60°,AD∥BC,
∴∠B′EF=∠EFB=∠B′FE=60°,
∴△B′EF为等边三角形,
∴∠EB′F=60°.
在Rt△A′B′E中,A′E=x,∠A′=90°,∠A′B′E=∠A′B′F-∠EB′F=30°,
∴EB′=2 A′E=2x,AE+ EB′=AB′,即x+2x=9,解得x=3,所以AE=A′E=3,EB′=6,
由勾股定理得:AB=A′B′=3,所以 S△EFB′′=![]() ×6×3
×6×3![]() =9
=9![]() .
.
故选:B.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目