题目内容
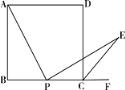
【题目】图①是一张∠AOB=45°的纸片折叠后的图形,P、Q分别是边OA、OB上的点,且OP=2 cm.将∠AOB沿PQ折叠,点O落在纸片所在平面内的C处.
(1)①当PC∥QB时,OQ= cm;
②在OB上找一点Q,使PC⊥QB(尺规作图,保留作图痕迹);
(2)当折叠后重叠部分为等腰三角形时,求OQ的长.
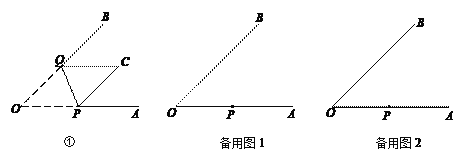
【答案】(1)2;见解析(2)当点C在∠AOB的内部或一边上时,则重叠部分即为△CPQ
【解析】分析:(1)①证明四边形,即可得OQ=OP=2cm;②分点C、P在BQ同侧和异侧两种情况作图即可;(3)当折叠后重叠部分为等腰三角形时,符合条件的点Q共有5个;点C在∠AOB的内部或一边上时,由折叠的性质、三角形内角和定理以及解直角三角形即可求出OQ的长;点C在∠AOB的外部时,同理求出OQ的长即可.
详解:
(1)①当PC∥QB时,∠O=∠CPA,
由折叠的性质得:∠C=∠O,OP=CP,
∴∠CPA=∠C,
∴OP∥QC,
∴四边形OPCQ是平行四边形,
∴四边形OPCQ是菱形,
∴OQ=OP=2cm;
故答案为:2cm;
② 分点C、P在BQ同侧和异侧两种情况,画对一种就给全分;
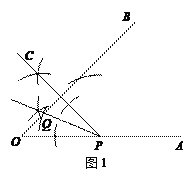
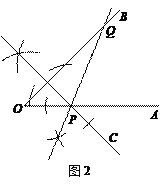
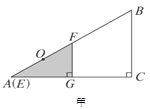
(2)当点C在∠AOB的内部或一边上时,则重叠部分即为△CPQ.
因为△CPQ是由△OPQ折叠得到,所以当△OPQ为等腰三角形时,重叠部分必为等腰三角形.
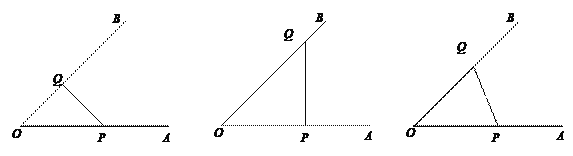 如图1、2、3三种情况:
如图1、2、3三种情况:


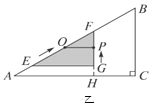
当点C在∠AOB的外部时,
当点C在射线OB的上方时(如图4), 当点C在射线OA的下方时(如图5),
OQ=![]() -
-![]() (cm)
(cm)
OQ=![]() +
+![]() (cm)
(cm)

【题目】元旦期间,某超市对出售![]() 、
、![]() 两种商品开展元旦促销活动,活动方案有如下两种:(同一种商品不可同时参与两种活动)
两种商品开展元旦促销活动,活动方案有如下两种:(同一种商品不可同时参与两种活动)
商品 |
|
| |
标价(单位:元) |
|
| |
方案一 | 每件商品出售价格 | 按标价降价 | 按标价降价 |
方案二 | 若所购商品超过 | ||
(1)某单位购买![]() 商品
商品![]() 件,
件,![]() 商品
商品![]() 件,共花费
件,共花费![]() 元,试求
元,试求![]() 的值;
的值;
(2)在(1)求出的![]() 值的条件下,若某单位购买
值的条件下,若某单位购买![]() 商品
商品![]() 件(
件(![]() 为正整数),购买
为正整数),购买![]() 商品的件数比
商品的件数比![]() 商品件数的
商品件数的![]() 倍还多一件,请问该单位选择哪种方案才能获得最大优惠?请说明理由.
倍还多一件,请问该单位选择哪种方案才能获得最大优惠?请说明理由.
【题目】河西中学九年级共有9个班,300名学生,学校要对该年级学生数学学科学业水平测试成绩进行抽样分析,请按要求回答下列问题:
收集数据
(1)若从所有成绩中抽取一个容量为36的样本,以下抽样方法中最合理的是 .
①在九年级学生中随机抽取36名学生的成绩;
②按男、女各随机抽取18名学生的成绩;
③按班级在每个班各随机抽取4名学生的成绩.
整理数据
(2)将抽取的36名学生的成绩进行分组,绘制频数分布表和成绩分布扇形统计图如下.请根据图表中数据填空:
①C类和D类部分的圆心角度数分别为 °、 °;
②估计九年级A、B类学生一共有 名.

成绩(单位:分) | 频数 | 频率 |
A类(80~100) | 18 |
|
B类(60~79) | 9 |
|
C类(40~59) | 6 |
|
D类(0~39) | 3 |
|
分析数据
(3)教育主管部门为了解学校教学情况,将河西、复兴两所中学的抽样数据进行对比,得下表:
学校 | 平均数(分) | 极差(分) | 方差 | A、B类的频率和 |
河西中学 | 71 | 52 | 432 | 0.75 |
复兴中学 | 71 | 80 | 497 | 0.82 |
你认为哪所学校本次测试成绩较好,请说明理由.