题目内容
【题目】如图,⊙O的直径AD长为6,AB是弦,∠A=30°,CD∥AB,且CD=![]() .
.
(1)求∠C的度数;
(2)求证:BC是⊙O的切线;
(3)求阴影部分面积.

【答案】(1)∠C=60°;(2)证明见解析;(3)S阴影=3π-![]() .
.
【解析】试题分析:(1)连接BD,由AD为圆的直径,得到∠ABD为直角,再利用30度角所对的直角边等于斜边的一半求出BD的长,根据CD与AB平行,得到一对内错角相等,确定出∠CDB为直角,在直角三角形BCD中,利用锐角三角函数定义求出tanC的值,即可确定出∠C的度数;
(2)连接OB,由OA=OB,利用等边对等角得到一对角相等,再由CD与AB平行,得到一对同旁内角互补,求出∠ABC度数,由∠ABC-∠ABO度数确定出∠OBC度数为90,即可得证;
(3)过O作OE⊥AB,利用30度角所对的直角边等于斜边的一半求出OE的长,根据勾股定理求出AE的长,进而求出AB的长,确定出三角形OAB面积,再由扇形AOB面积减去三角形AOB面积求出阴影部分面积即可.
试题解析:(1)如图,连接BD,
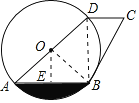
∵AD为圆O的直径,
∴∠ABD=90°,
∴BD=![]() AD=3,
AD=3,
∵CD∥AB,∠ABD=90°,
∴∠CDB=∠ABD=90°,
在Rt△CDB中,tanC=![]() =
=![]() =
=![]() ,
,
∴∠C=60°;
(2)证明:连接OB,
∵OA=OB,
∴∠OBA=∠A=30°,
∵CD∥AB,∠C=60°,
∴∠ABC=180°-∠C=120°,
∴∠OBC=∠ABC-∠ABO=120°-30°=90°,
∴OB⊥BC,
∴BC为圆O的切线;
(3)解:过点O作OE⊥AB,则有OE=![]() OA=
OA=![]() ,
,
∵AB=![]() =
=![]() =3
=3![]() ,
,
∴S△OAB=![]() ABOE=
ABOE=![]() ×3
×3![]() ×
×![]() =
=![]() ,
,
∵∠AOB=180°-2∠A=120°,
∴S扇形OAB=![]() =3π,
=3π,
则S阴影=S扇形OAB-S△AOB=3π-![]() .
.

【题目】某市在艺术节中组织中小学校文艺汇演,甲、乙两所学校共92名学生![]() 其中甲校学生多于乙校学生,且甲校学生不足90名
其中甲校学生多于乙校学生,且甲校学生不足90名![]() ,现准备统一购买服装参加演出,下表是某服装厂给出的演出服装价格表:
,现准备统一购买服装参加演出,下表是某服装厂给出的演出服装价格表:
购买服装的套数 | 1套至45套 | 46套至90套 | 91套及以上 |
每套服装的价格 | 60元 | 50元 | 40元 |
如果两所学校单独购买服装,一共应付5000元
(1)甲、乙两校各有多少名学生准备参加汇演?
(2)如果甲、乙两校联合起来购买服装,那么比各自购买服装共可以节省多少钱?
(3)如果甲校有10名学生被调去参加书法绘画比赛不能参加演出,请你为两校设计购买服装方案,并说明哪一种最省钱.