题目内容
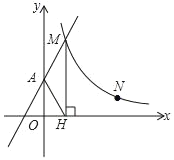
【题目】已知抛物线![]() 的开口向上顶点为P
的开口向上顶点为P
(1)若P点坐标为(4,一1),求抛物线的解析式;
(2)若此抛物线经过(4,一1),当-1≤x≤2时,求y的取值范围(用含a的代数式表示)
(3)若a=1,且当0≤x≤1时,抛物线上的点到x轴距离的最大值为6,求b的值
【答案】(1)![]() ;(2)1-4a≤y≤4+5a;(3)b=2或-10.
;(2)1-4a≤y≤4+5a;(3)b=2或-10.
【解析】
(1)将P(4,-1)代入,可求出解析式
(2)将(4,-1)代入求得:b=-4a-1,再代入对称轴直线![]() 中,可判断
中,可判断![]() ,且开口向上,所以y随x的增大而减小,再把x=-1,x=2代入即可求得.
,且开口向上,所以y随x的增大而减小,再把x=-1,x=2代入即可求得.
(3)观察图象可得,当0≤x≤1时,抛物线上的点到x轴距离的最大值为6,这些点可能为x=0,x=1,![]() 三种情况,再根据对称轴
三种情况,再根据对称轴![]() 在不同位置进行讨论即可.
在不同位置进行讨论即可.
解:(1)由此抛物线顶点为P(4,-1),
所以y=a(x-4)2-1=ax2-8ax+16a-1,即16a-1=3,解得a=![]() , b=-8a=-2
, b=-8a=-2
所以抛物线解析式为:![]() ;
;
(2)由此抛物线经过点C(4,-1),
所以 一1=16a+4b+3,即b=-4a-1.
因为抛物线![]() 的开口向上,则有
的开口向上,则有![]()
其对称轴为直线![]() ,而
,而![]()
所以当-1≤x≤2时,y随着x的增大而减小
当x=-1时,y=a+(4a+1)+3=4+5a
当x=2时,y=4a-2(4a+1)+3=1-4a
所以当-1≤x≤2时,1-4a≤y≤4+5a;
(3)当a=1时,抛物线的解析式为y=x2+bx+3
∴抛物线的对称轴为直线![]()
由抛物线图象可知,仅当x=0,x=1或x=-![]() 时,抛物线上的点可能离x轴最远
时,抛物线上的点可能离x轴最远
分别代入可得,当x=0时,y=3
当x=1时,y=b+4
当x=-![]() 时,y=-
时,y=-![]() +3
+3
①当一![]() <0,即b>0时,3≤y≤b+4,
<0,即b>0时,3≤y≤b+4,
由b+4=6解得b=2
②当0≤-![]() ≤1时,即一2≤b≤0时,△=b2-12<0,抛物线与x轴无公共点
≤1时,即一2≤b≤0时,△=b2-12<0,抛物线与x轴无公共点
由b+4=6解得b=2(舍去);
③当![]() ,即b<-2时,b+4≤y≤3,
,即b<-2时,b+4≤y≤3,
由b+4=-6解得b=-10
综上,b=2或-10

 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案