��Ŀ����
��֪��������ABCD�У�AD��BC��AB=AD=DC=5��cos��ABC=
����E��AB�ߵ��е㣬��F������BC�ϵ�һ���㣬����BD��DF��
��1����ͼ1����DF��BCʱ����tan��ABD��
��2����ͼ2������F��BC���ӳ�����ʱ������EF����DC���ڵ�G����CF=m�������߶�DG���ú�m�Ĵ���ʽ��ʾ����
��3����M�DZ�DC��һ�㣬��5DM=8AE������AM����Խ���BD�ཻ�ڵ�N������BDF�ס�ADN�������߶�CF��

| 3 | 5 |
��1����ͼ1����DF��BCʱ����tan��ABD��
��2����ͼ2������F��BC���ӳ�����ʱ������EF����DC���ڵ�G����CF=m�������߶�DG���ú�m�Ĵ���ʽ��ʾ����
��3����M�DZ�DC��һ�㣬��5DM=8AE������AM����Խ���BD�ཻ�ڵ�N������BDF�ס�ADN�������߶�CF��

��������1���ȸ��ݵȵԵȽǣ�ƽ���ߵ����ʼ����Ǻ�����֪ʶ�������tan��ABD��
��2������E��EN��BC������G��GM��BC������A��AP��BC������D��DQ��BC������ƽ���ߵ��ж������������ε����ʼ�������߶�DG��
��3������A��AH��BC�ڵ�H����HCΪx�ᣬHAΪy�Ὠ��ֱ������ϵ������M��MP��BC�ڵ�P������D��DQ��BC�ڵ�Q���������������ε����ʽ�������ε������ʽ������⣮
��2������E��EN��BC������G��GM��BC������A��AP��BC������D��DQ��BC������ƽ���ߵ��ж������������ε����ʼ�������߶�DG��
��3������A��AH��BC�ڵ�H����HCΪx�ᣬHAΪy�Ὠ��ֱ������ϵ������M��MP��BC�ڵ�P������D��DQ��BC�ڵ�Q���������������ε����ʽ�������ε������ʽ������⣮
����⣺��1����AB=AD��
���ABD=��ADB��
��AD��BC��
���ADB=��DBC��
���ABD=��DBC��
tan��ABD=tan��
��ABC��=
=
��
 ��2������E��EN��BC������G��GM��BC������A��AP��BC������D��DQ��BC
��2������E��EN��BC������G��GM��BC������A��AP��BC������D��DQ��BC
����EN��GM��AP��QD
����GM��EN=FM��FN��
����EN=
AP=
DQ��
��2GM��DQ=FM��FN
GM��DQ=CG��CD=CM��CQ
��2CM��CQ=FM��FN=��FC+CM������BF-BN��=��m+CM������11+m-
��=2CM��CQ=2CM��3
���CM=
��
CG��CD=CM��CQ
��CD-DG����CD=CM��CQ
����5-DG����5=
��3��
���DG=
��
��3������A��AH��BC�ڵ�H����HCΪx�ᣬHAΪy�Ὠ��ֱ������ϵ����M��MP��BC�ڵ�P������D��DQ��BC�ڵ�Q
��CP��CQ=MP��DQ=CM��CD
5DM=8AE=8��5��2=20��DM=4��
��CP��CQ=MP��DQ=��5-4����5
��CP=
��MP=
��
���A��0��4������M��
��
������B��-3��0������D��5��4��
ֱ��AMΪy=-
x+4��ֱ��BDΪy=
x+
��
��ֱ���ཻ�ڵ�N����NΪ��
��
��
��AND�У��ױ�AD=5��h=4-
=
��
S=0.5��5��
=
=S��BDF=0.5��4BF
BF=
��
CF=BC-BF=3+5+3-
=
��
���ABD=��ADB��
��AD��BC��
���ADB=��DBC��
���ABD=��DBC��
tan��ABD=tan��
| 1 |
| 2 |
|
| 1 |
| 2 |
 ��2������E��EN��BC������G��GM��BC������A��AP��BC������D��DQ��BC
��2������E��EN��BC������G��GM��BC������A��AP��BC������D��DQ��BC����EN��GM��AP��QD
����GM��EN=FM��FN��
����EN=
| 1 |
| 2 |
| 1 |
| 2 |
��2GM��DQ=FM��FN
GM��DQ=CG��CD=CM��CQ
��2CM��CQ=FM��FN=��FC+CM������BF-BN��=��m+CM������11+m-
| 3 |
| 2 |
���CM=
| 3m |
| 16+2m |
CG��CD=CM��CQ
��CD-DG����CD=CM��CQ
����5-DG����5=
| 3m |
| 16+2m |
���DG=
| 5(16+m) |
| 16+2m |
��3������A��AH��BC�ڵ�H����HCΪx�ᣬHAΪy�Ὠ��ֱ������ϵ����M��MP��BC�ڵ�P������D��DQ��BC�ڵ�Q
��CP��CQ=MP��DQ=CM��CD
5DM=8AE=8��5��2=20��DM=4��
��CP��CQ=MP��DQ=��5-4����5
��CP=
| 3 |
| 5 |
| 4 |
| 5 |
���A��0��4������M��
| 37 |
| 5 |
| 4 |
| 5 |
ֱ��AMΪy=-
| 16 |
| 37 |
| 1 |
| 2 |
| 3 |
| 2 |
��ֱ���ཻ�ڵ�N����NΪ��
| 185 |
| 69 |
| 196 |
| 69 |
��AND�У��ױ�AD=5��h=4-
| 196 |
| 69 |
| 80 |
| 69 |
S=0.5��5��
| 80 |
| 69 |
| 200 |
| 69 |
BF=
| 100 |
| 69 |
CF=BC-BF=3+5+3-
| 100 |
| 69 |
| 659 |
| 69 |
�������������������ۺ��⣬�����漰��֪ʶ���е��������ε����ʣ�ƽ���ߵ����ʣ����Ǻ��������������ε����ʺ������ε�������ۺ��Խ�ǿ����һ�����Ѷȣ�

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
 ��֪��������ABCD�У�AD��BC����E��AB�ϣ���F��DC�ϣ���AD=a��BC=b��
��֪��������ABCD�У�AD��BC����E��AB�ϣ���F��DC�ϣ���AD=a��BC=b��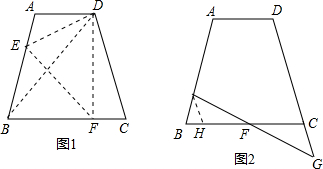
 ��ͼ����֪��������ABCD�У�AD��BC��AD=3��BC=5����E��AB�ϣ���AE��EB=2��3������E��EF��BC��CD��F����EF�ij���
��ͼ����֪��������ABCD�У�AD��BC��AD=3��BC=5����E��AB�ϣ���AE��EB=2��3������E��EF��BC��CD��F����EF�ij��� ��֪��������ABCD�У�AD��BC��AB=DC=5��AD=3.5��
��֪��������ABCD�У�AD��BC��AB=DC=5��AD=3.5�� ��֪��������ABCD�У�AD��BC����ABC=90�㣬BC=2AD����E��F�ֱ���BC��DC���е㣬����AE��EF��BD��AE��BD�ཻ�ڵ�G��
��֪��������ABCD�У�AD��BC����ABC=90�㣬BC=2AD����E��F�ֱ���BC��DC���е㣬����AE��EF��BD��AE��BD�ཻ�ڵ�G��