题目内容
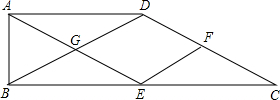 已知,在梯形ABCD中,AD∥BC,∠ABC=90°,BC=2AD,点E、F分别是BC和DC的中点,连接AE、EF和BD,AE和BD相交于点G.
已知,在梯形ABCD中,AD∥BC,∠ABC=90°,BC=2AD,点E、F分别是BC和DC的中点,连接AE、EF和BD,AE和BD相交于点G.(1)求证:四边形AECD是平行四边形;
(2)求证:四边形EFDG是菱形.
分析:(1)因为AD∥BC,若要四边形AECD是平行四边形,即证明AD=CE即可;
(2)连接DE,易得四边形ABED是平行四边形,又由∠ABE=90°,可证得四边形ABED是矩形,根据矩形的性质,易证得EF=GD=GE=DF,则可得四边形EFDG是菱形.
(2)连接DE,易得四边形ABED是平行四边形,又由∠ABE=90°,可证得四边形ABED是矩形,根据矩形的性质,易证得EF=GD=GE=DF,则可得四边形EFDG是菱形.
解答:证明:(1)∵点E是BC的中点,
∴EC=BE=
BC,
∵BC=2AD,
∴EC=AD,
∵AD∥EC,
∴四边形AECD为平行四边形;
(2)连接DE,
∵AD∥BE,AD=BE,
∴四边形ABED是平行四边形,
又∵∠ABE=90°,
∴□ABED是矩形
∴BD=AE,GE=GA=
AE,GB=GD=
BD
∴GE=GD,
∵E、F分别是BC、CD的中点
∴EF、GE是△CBD的两条中位线,
∴EF=
BD=GD,GE=
CD=DF,
∴EF=GD=GE=DF,
∴四边形EFDG是菱形.

∴EC=BE=
| 1 |
| 2 |
∵BC=2AD,
∴EC=AD,
∵AD∥EC,
∴四边形AECD为平行四边形;
(2)连接DE,
∵AD∥BE,AD=BE,
∴四边形ABED是平行四边形,
又∵∠ABE=90°,
∴□ABED是矩形
∴BD=AE,GE=GA=
| 1 |
| 2 |
| 1 |
| 2 |
∴GE=GD,
∵E、F分别是BC、CD的中点
∴EF、GE是△CBD的两条中位线,
∴EF=
| 1 |
| 2 |
| 1 |
| 2 |
∴EF=GD=GE=DF,
∴四边形EFDG是菱形.
点评:此题考查了平行四边形的判定与性质,矩形与菱形的判定与性质等知识.此题综合性较强,难度适中,解题的关键是要注意数形结合思想的应用.

练习册系列答案
相关题目
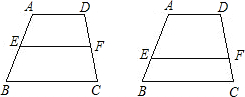 已知:在梯形ABCD中,AD∥BC,点E在AB上,点F在DC上,且AD=a,BC=b.
已知:在梯形ABCD中,AD∥BC,点E在AB上,点F在DC上,且AD=a,BC=b.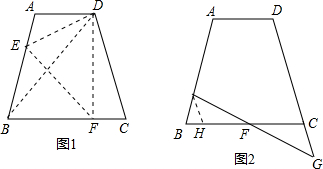
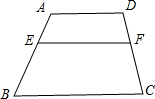 如图,已知:在梯形ABCD中,AD∥BC,AD=3,BC=5,点E在AB上,且AE:EB=2:3,过点E作EF∥BC交CD于F,求EF的长?
如图,已知:在梯形ABCD中,AD∥BC,AD=3,BC=5,点E在AB上,且AE:EB=2:3,过点E作EF∥BC交CD于F,求EF的长? 已知:在梯形ABCD中,AD∥BC,AB=DC=5,AD=3.5,
已知:在梯形ABCD中,AD∥BC,AB=DC=5,AD=3.5,