题目内容
已知:在梯形ABCD中,AD∥BC,AB=DC,E,F分别是AB和BC边上的点.(1)如图①,以EF为对称轴翻折梯形ABCD,使点B与点D重合,且DF⊥BC.若AD=4,BC=8,求梯形ABCD的面积S梯形ABCD的值;
(2)如图②,连接EF并延长与DC的延长线交于点G,如果FG=k•EF(k为正数),试猜想BE与CG有何数量关系写出你的结论并证明之.
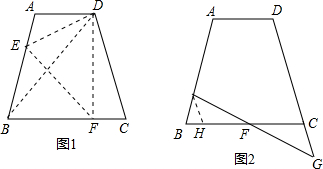
分析:(1)由折叠的性质知,BF=DF,过点A作AG⊥BC于点G.则四边形AGFD是矩形,然后根据相似三角形的特点,利用面积公式求出.
(2)如图,过点E作EH∥CG,交BC于点H.则∠FEH=∠FGC,可得△EFH∽△GFC.根据相似三角形和梯形的性质解决.
(2)如图,过点E作EH∥CG,交BC于点H.则∠FEH=∠FGC,可得△EFH∽△GFC.根据相似三角形和梯形的性质解决.
解答: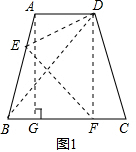 解:(1)由题意,有△BEF≌△DEF.
解:(1)由题意,有△BEF≌△DEF.
∴BF=DF
如图,过点A作AG⊥BC于点G.则四边形AGFD是矩形.
∴AG=DF,GF=AD=4.
在Rt△ABG和Rt△DCF中,
∵AB=DC,AG=DF,
∴Rt△ABG≌Rt△DCF.(HL)
∴BG=CF
∴BG=
(BC-GF)=
(8-4)=2.
∴DF=BF=BG+GF=2+4=6
∴S梯形ABCD=
(AD+BC)•DF=
×(4+8)×6=36
(2)猜想:CG=k•BE(或BE=
CG)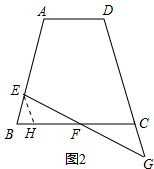
证明:如图,过点E作EH∥CG,交BC于点H.
则∠FEH=∠FGC.
又∠EFH=∠GFC,
∴△EFH∽△GFC.
∴
=
,
而FG=k•EF,即
=k.
∴
=
即CG=k•EH
∵EH∥CG,∴∠EHB=∠DCB.
而四边形ABCD是等腰梯形,∴∠B=∠DCB.
∴∠B=∠EHB.∴BE=EH.
∴CG=k•BE.
 解:(1)由题意,有△BEF≌△DEF.
解:(1)由题意,有△BEF≌△DEF.∴BF=DF
如图,过点A作AG⊥BC于点G.则四边形AGFD是矩形.
∴AG=DF,GF=AD=4.
在Rt△ABG和Rt△DCF中,
∵AB=DC,AG=DF,
∴Rt△ABG≌Rt△DCF.(HL)
∴BG=CF
∴BG=
| 1 |
| 2 |
| 1 |
| 2 |
∴DF=BF=BG+GF=2+4=6
∴S梯形ABCD=
| 1 |
| 2 |
| 1 |
| 2 |
(2)猜想:CG=k•BE(或BE=
| 1 |
| K |

证明:如图,过点E作EH∥CG,交BC于点H.
则∠FEH=∠FGC.
又∠EFH=∠GFC,
∴△EFH∽△GFC.
∴
| EF |
| GF |
| EH |
| GC |
而FG=k•EF,即
| GF |
| EF |
∴
| EH |
| GC |
| 1 |
| k |
∵EH∥CG,∴∠EHB=∠DCB.
而四边形ABCD是等腰梯形,∴∠B=∠DCB.
∴∠B=∠EHB.∴BE=EH.
∴CG=k•BE.
点评:本题利用了:1、折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等;
2、等腰梯形的性质,全等三角形和相似三角形的判定和性质求解
2、等腰梯形的性质,全等三角形和相似三角形的判定和性质求解

练习册系列答案
相关题目
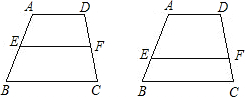 已知:在梯形ABCD中,AD∥BC,点E在AB上,点F在DC上,且AD=a,BC=b.
已知:在梯形ABCD中,AD∥BC,点E在AB上,点F在DC上,且AD=a,BC=b.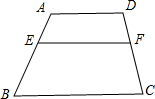 如图,已知:在梯形ABCD中,AD∥BC,AD=3,BC=5,点E在AB上,且AE:EB=2:3,过点E作EF∥BC交CD于F,求EF的长?
如图,已知:在梯形ABCD中,AD∥BC,AD=3,BC=5,点E在AB上,且AE:EB=2:3,过点E作EF∥BC交CD于F,求EF的长? 已知:在梯形ABCD中,AD∥BC,AB=DC=5,AD=3.5,
已知:在梯形ABCD中,AD∥BC,AB=DC=5,AD=3.5, 已知,在梯形ABCD中,AD∥BC,∠ABC=90°,BC=2AD,点E、F分别是BC和DC的中点,连接AE、EF和BD,AE和BD相交于点G.
已知,在梯形ABCD中,AD∥BC,∠ABC=90°,BC=2AD,点E、F分别是BC和DC的中点,连接AE、EF和BD,AE和BD相交于点G.