题目内容
 已知:在梯形ABCD中,AD∥BC,AB=DC=5,AD=3.5,sinB=
已知:在梯形ABCD中,AD∥BC,AB=DC=5,AD=3.5,sinB=| 4 | 5 |
(1)求BC的长;
(2)试求y关于x的函数关系式,并写出定义域;
(3)连接EF,如果△PEF是等腰三角形,试求BP的长.
分析:(1)作等腰梯形ABCD的高AM、DN,得矩形AMND,△ABM≌△DCN,则BC=BM+MN+NC=AD+2AB•cosB=9.5;
(2)先由三角形内角和定理得出∠BEP=∠GPC,由等腰梯形在同一底上的两个角相等得出∠B=∠C,则△BEP∽△CPG,根据相似三角形对应边成比例得出y关于x的函数关系式,并写出定义域;
(3)分三种情况:①PE=PF;②PE=EF;③PF=EF.
(2)先由三角形内角和定理得出∠BEP=∠GPC,由等腰梯形在同一底上的两个角相等得出∠B=∠C,则△BEP∽△CPG,根据相似三角形对应边成比例得出y关于x的函数关系式,并写出定义域;
(3)分三种情况:①PE=PF;②PE=EF;③PF=EF.
解答: 解:(1)如图,作等腰梯形ABCD的高AM、DN,得矩形AMND,△ABM≌△DCN,
解:(1)如图,作等腰梯形ABCD的高AM、DN,得矩形AMND,△ABM≌△DCN,
所以BC=BM+MN+NC=AD+2AB•cosB=3.5+2×5×
=9.5;
(2)如图.∵∠EPB+∠EPF+∠GPC=∠EPB+∠B+∠BEP=180°,∠EPF=∠B,
∴∠BEP=∠GPC,
∵ABCD是等腰梯形,
∴∠B=∠C,
∴△BEP∽△CPG,
 ∴BE:CP=BP:CG,
∴BE:CP=BP:CG,
∴3:(9.5-x)=x:CG ①;
又∵FD∥PC,
∴△GFD∽△GPC,
∴FD:PC=GD:GC,
∴y:(9.5-x)=(CG-5):CG ②,
①②联立,消去CG,解得y=9.5-x-
,
∵射线PF与AD边交于点F,即y>0,
∴9.5-x-
>0,
又x>0,
∴9.5x-x2-15>0,
∴x2-9.5x+15>0,
解得2<x<7.5;
 (3)分三种情况:
(3)分三种情况:
①如果PE=PF,如图,过F作DC平行线交底边于H,则∠FHP=∠C=∠B.
∵在△PEB与△FPH中,
,
∴△PEB≌△FPH(AAS),
∴EB=PH=3,BP=FH=DC=5;
 ②如果PE=EF,如图,过F作DC平行线交底边于H,则∠FHP=∠C=∠B.
②如果PE=EF,如图,过F作DC平行线交底边于H,则∠FHP=∠C=∠B.
∵在△PEB与△FPH中,
,
∴△PEB∽△FPH,
∴PE:PF=PB:FH,
又∵PE=EF,
过E点做△EFP的高ET,则FP:PE=2PT:PE=2cos∠EPF=2cos∠B=
,
∵FH=DC=5,
∴
=
,
解得x=
;
 ③如果PF=EF,同理可得△PEB∽△FPH,
③如果PF=EF,同理可得△PEB∽△FPH,
∴PE:PF=PB:FH,
∵PE=EF,
过F点做△EFP的高FT,则PE:PF=2PT:PF=2cos∠EPF=2cosB=
,
∵FH=DC=5,
∴
=
,
解得x=6.
 解:(1)如图,作等腰梯形ABCD的高AM、DN,得矩形AMND,△ABM≌△DCN,
解:(1)如图,作等腰梯形ABCD的高AM、DN,得矩形AMND,△ABM≌△DCN,所以BC=BM+MN+NC=AD+2AB•cosB=3.5+2×5×
| 3 |
| 5 |
(2)如图.∵∠EPB+∠EPF+∠GPC=∠EPB+∠B+∠BEP=180°,∠EPF=∠B,
∴∠BEP=∠GPC,
∵ABCD是等腰梯形,
∴∠B=∠C,
∴△BEP∽△CPG,
 ∴BE:CP=BP:CG,
∴BE:CP=BP:CG,∴3:(9.5-x)=x:CG ①;
又∵FD∥PC,
∴△GFD∽△GPC,
∴FD:PC=GD:GC,
∴y:(9.5-x)=(CG-5):CG ②,
①②联立,消去CG,解得y=9.5-x-
| 15 |
| x |
∵射线PF与AD边交于点F,即y>0,
∴9.5-x-
| 15 |
| x |
又x>0,
∴9.5x-x2-15>0,
∴x2-9.5x+15>0,
解得2<x<7.5;
 (3)分三种情况:
(3)分三种情况:①如果PE=PF,如图,过F作DC平行线交底边于H,则∠FHP=∠C=∠B.
∵在△PEB与△FPH中,
|
∴△PEB≌△FPH(AAS),
∴EB=PH=3,BP=FH=DC=5;
 ②如果PE=EF,如图,过F作DC平行线交底边于H,则∠FHP=∠C=∠B.
②如果PE=EF,如图,过F作DC平行线交底边于H,则∠FHP=∠C=∠B.∵在△PEB与△FPH中,
|
∴△PEB∽△FPH,
∴PE:PF=PB:FH,
又∵PE=EF,
过E点做△EFP的高ET,则FP:PE=2PT:PE=2cos∠EPF=2cos∠B=
| 6 |
| 5 |
∵FH=DC=5,
∴
| 5 |
| 6 |
| x |
| 5 |
解得x=
| 25 |
| 6 |
 ③如果PF=EF,同理可得△PEB∽△FPH,
③如果PF=EF,同理可得△PEB∽△FPH,∴PE:PF=PB:FH,
∵PE=EF,
过F点做△EFP的高FT,则PE:PF=2PT:PF=2cos∠EPF=2cosB=
| 6 |
| 5 |
∵FH=DC=5,
∴
| 5 |
| 6 |
| 5 |
| x |
解得x=6.
点评:本题考查了等腰梯形的性质,全等三角形、相似三角形的判定与性质,等腰三角形的性质,第(3)问进行分类讨论是解题的关键.

练习册系列答案
 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
 已知:在梯形ABCD中,AD∥BC,点E在AB上,点F在DC上,且AD=a,BC=b.
已知:在梯形ABCD中,AD∥BC,点E在AB上,点F在DC上,且AD=a,BC=b.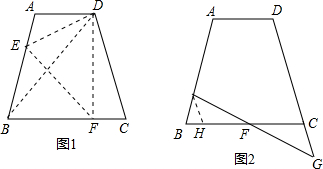
 如图,已知:在梯形ABCD中,AD∥BC,AD=3,BC=5,点E在AB上,且AE:EB=2:3,过点E作EF∥BC交CD于F,求EF的长?
如图,已知:在梯形ABCD中,AD∥BC,AD=3,BC=5,点E在AB上,且AE:EB=2:3,过点E作EF∥BC交CD于F,求EF的长? 已知,在梯形ABCD中,AD∥BC,∠ABC=90°,BC=2AD,点E、F分别是BC和DC的中点,连接AE、EF和BD,AE和BD相交于点G.
已知,在梯形ABCD中,AD∥BC,∠ABC=90°,BC=2AD,点E、F分别是BC和DC的中点,连接AE、EF和BD,AE和BD相交于点G.