题目内容
【题目】如图,矩形OABC的顶点A、C坐标分别是(8,0),(0,4),反比例函数y= ![]() (x>0)的图象过对角线的交点P并且与AB、BC分别交于D、E两点,连接OD、OE、DE,则△ODE的面积为( )
(x>0)的图象过对角线的交点P并且与AB、BC分别交于D、E两点,连接OD、OE、DE,则△ODE的面积为( ) 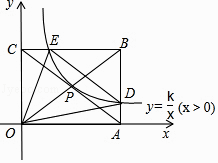
A.14
B.12
C.15
D.8
【答案】C
【解析】解:∵矩形OABC的顶点A、C坐标分别是(8,0),(0,4), ∴P(4,2),
∵反比例函数y= ![]() (x>0)的图象过对角线的交点P,
(x>0)的图象过对角线的交点P,
∴k=4×2=8,
∴反比例函数为y= ![]() ,
,
当y=4时,x=2;当x=8时,x=1,
∴E(2,4),D(8,1),
∴CE=2,BE=6,AD=1,BD=3,
∴△ODE的面积=矩形AOCB的面积﹣△AOD的面积﹣△COE的面积﹣△BDE的面积
=8×4﹣ ![]() ×8×1﹣
×8×1﹣ ![]() ×2×4﹣
×2×4﹣ ![]() ×3×6
×3×6
=32﹣4﹣4﹣9
=15,
故选:C.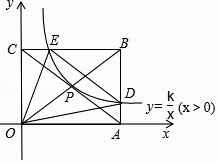
先根据反比例函数y= ![]() (x>0)的图象过对角线的交点P,求得反比例函数为y=
(x>0)的图象过对角线的交点P,求得反比例函数为y= ![]() ,进而得到E(2,4),D(8,1),最后根据△ODE的面积=矩形AOCB的面积﹣△AOD的面积﹣△COE的面积﹣△BDE的面积,进行计算即可.
,进而得到E(2,4),D(8,1),最后根据△ODE的面积=矩形AOCB的面积﹣△AOD的面积﹣△COE的面积﹣△BDE的面积,进行计算即可.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目