题目内容
【题目】如图1,抛物线y=![]() x2﹣
x2﹣![]() (m﹣1)x﹣
(m﹣1)x﹣![]() m(m>0)与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,且OB=3OA.
m(m>0)与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,且OB=3OA.
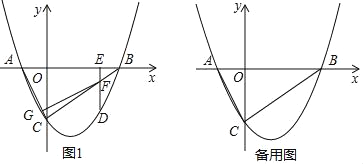
(1)求该抛物线的函数表达式;
(2)动点D在线段BC下方的抛物线上.
①连接AC、BC,过点D作x轴的垂线,垂足为E,交BC于点F.过点F作FG⊥AC,垂足为G.设点D的横坐标为t,线段FG的长为d,用含t的代数式表示d;
②过点D作DH⊥BC,垂足为H,连接CD.是否存在点D,使得△CDH中的一个角恰好等于∠ABC的2倍?如果存在,求出点D的横坐标;如果不存在,请说明理由.
【答案】(1)y=![]() x2﹣
x2﹣![]() x﹣2;(2)①d=
x﹣2;(2)①d=![]() t;②存在;D的横坐标为
t;②存在;D的横坐标为![]() 或1
或1
【解析】
(1)根据题意可求点A(-1,0),点B(m,0),根据OB=3OA,可求m的值,即可求解析式;
(2)①先求出直线BC解析式,即可得F点坐标,利用S△AFC=S△ABC-S△ABF.可得用含t的代数式表示d;
②分∠CDH=2∠ABC或∠DCH=2∠ABC两种情况讨论,利用锐角三角函数,相似三角形的性质可求点D的横坐标.
(1)令y=0,则0=![]() x2﹣
x2﹣![]() (m﹣1)x﹣
(m﹣1)x﹣![]() m,
m,
∴x2﹣(m﹣1)x﹣m=0,
∴(x﹣m)(x+1)=0,
∴x1=m,x2=﹣1,
∵m>0,点A在点B的左侧,
∴点A(﹣1,0),点B(m,0),
∴OA=1,OB=m,
∵OB=3OA,
∴m=3,
∴抛物线y=![]() x2﹣
x2﹣![]() x﹣2,
x﹣2,
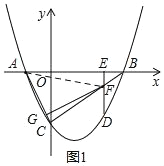
(2)①如图1:连接AF,
∵抛物线y=![]() x2﹣
x2﹣![]() x﹣2与y轴交与点C,
x﹣2与y轴交与点C,
∴点C(0,﹣2),
∵点A(﹣1,0),点B(3,0),点C(0,﹣2),
∴AB=4,OC=2,AC=![]()
∵设直线BC解析式y=kx+b.
∴![]()
解得:b=﹣2,b=![]()
∴直线BC解析式y=![]() x﹣2,
x﹣2,
∵D点横坐标为t,DF⊥AB,
∴点F的横坐标为t,
∴F(t,![]() t﹣2),
t﹣2),
∵S△AFC=S△ABC﹣S△ABF.
∴![]()
∴![]()
∴d=![]()
②若∠DCH=2∠ABC,如图2:过点C作CF∥AB,交抛物线于F点,作DE⊥CF于点E.
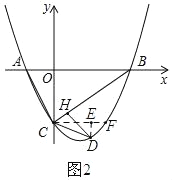
∵AB∥CF,
∴∠ABC=∠BCF,
又∵∠DCH=2∠BCF,
∴∠DCF=∠ABC=∠BCF,
∵点D坐标为(t,![]() t2﹣
t2﹣![]() t﹣2),
t﹣2),
∴CE=t,DE=﹣2﹣(![]() t2﹣
t2﹣![]() t﹣2)=
t﹣2)=![]() t﹣
t﹣![]() t2.
t2.
∵tan∠DCF=tan∠ABC=![]()
∴![]()
∴t1=0(不合题意舍去),t2=1,
即点D的横坐标为1.
若∠CDH=2∠ABC,如图3:作∠ECB=∠ABC,过点B作BP∥HD,交CD的延长线于点P,作PF⊥AB于F.
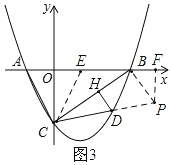
∵∠ECB=∠ABC,
∴EC=BE,∠AEC=2∠ABC,
在Rt△OEC中,CE2=OE2+OC2.
∴CE2=(3﹣CE)2+4,
∴CE=![]()
∴OE=OB﹣BE=![]()
∴tan∠AEC=tan2∠ABC=![]()
∵点B(3,0),点C(0,﹣2),
∴BC=![]()
∵BP∥HD,HD⊥BC,
∴BP⊥BC,∠CDH=∠CPB=2∠ABC,
∴tan∠CPB=tan2∠ABC=![]()
∴BP=![]()
∵∠ABC+∠PBF=90°,∠ABC+∠OCB=90°,
∴∠OCB=∠PBF,且∠BOC=∠PFB=90°,
∴△BOC∽△PFB,
∴![]()
∴PF=![]() ,BF=
,BF=![]()
∴OF=3+![]() =
=![]()
∴点P坐标(![]() ,﹣
,﹣![]() ),
),
∵点C(0,﹣2),点P(![]() ,﹣
,﹣![]() ),
),
∴直线PC解析式y=![]() x﹣2,
x﹣2,
∵直线CP与抛物线交于C,D两点,
∴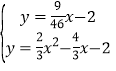
解得:x1=0,x2=![]()
∴点D的横坐标为![]()
综上所述:点D的横坐标为![]() 或1,
或1,