Question

【题目】如图，小强在河的一边，要测河面的一只船B与对岸码头A的距离，他的做法如下：

①在岸边确定一点C，使C与A，B在同一直线上；

②在AC的垂直方向画线段CD，取其中点O；

③画DF⊥CD使F、O、A在同一直线上；

④在线段DF上找一点E，使E与O、B共线．

他说测出线段EF的长就是船B与码头A的距离．他这样做有道理吗？为什么？

Answer 1

【答案】有道理，见解析

【解析】

试题分析：首先证明△ACO≌△FDO，根据全等三角形的性质可得AO=FO，∠A=∠F，再证明△ABO≌△FEO，进而可得EF=AB．

解：有道理，

∵DF⊥CD，AC⊥CD，

∴∠C=∠D=90°，

∵O为CD中点，

∴CO=DO，

在△ACO和△FDO中，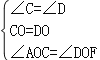

∴△ACO≌△FDO（ASA），

∴AO=FO，∠A=∠F，

在△ABO和△EOF中，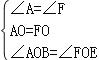

∴△ABO≌△FEO（ASA），

∴EF=AB．