题目内容
【题目】如图,AB是⊙O的直径,点P是y轴正半轴上的一点,⊙O与y轴正半轴交于点C,PB交⊙O于点D,点D是劣弧![]() 的中点,AB=
的中点,AB=![]() .
.
(1)求 P点的坐标及![]() 的值;
的值;
(2)求证:DP2=OP·CP.

【答案】(1)点P的坐标为(0, ![]() ),1;(2)证明见解析.
),1;(2)证明见解析.
【解析】分析:(1) 作DF⊥OB, DE⊥OC,由题中条件得出△PED∽△POB,而后求出点P的坐标,再利用解直角三角形得出结果.(2)用(1)的方法可得△PCD∽△PDO 从而求解.
本题解析:(1)如图, 作DF⊥OB, DE⊥OC,垂足分别为F、E
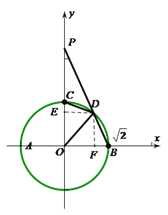
∵点D是劣弧![]() 的中点,∴∠EOD=45°
的中点,∴∠EOD=45°
在Rt△DEO中DO=![]() ,∴DE=EO=1
,∴DE=EO=1
∵ED∥OB,∴△PED∽△POB
∴![]() ∴
∴![]()
∴![]()
∴![]()
∴点P的坐标为(0, ![]() ),
),
∵∠DOF=∠EOD=45°,OD=OB
∴∠OBD=∠ODB=![]()
∴∠OPB=90O-67.5O=22.5O
∴![]() =
= ![]() ,
,
(2) 同上:∠OCD=∠ODC=![]()
∴∠PCD=180O-67.5O=122.5O,
∠PDO=180O-∠ODB= 180O-67.5O=122.5O,
∴△PCD∽△PDO
∴![]()
∴DP2=OP·CP;

练习册系列答案
相关题目