题目内容
【题目】如图,线段AC=n+1(其中n为正整数),点B在线段AC上,在线段AC同侧作正方形ABMN及正方形BCEF,连接AM、ME、EA得到△AME.当AB=1时,△AME的面积记为S1;当AB=2时,△AME的面积记为S2;…;当AB=n时,△AME的面积记为Sn.则Sn= ![]() n2 .
n2 .
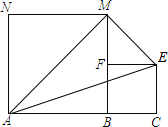
【答案】![]() n2
n2
【解析】
试题分析:将△AME的面积表示为长方形减去三个三角形的形式,根据题意,找出各边长度,根据长方形的面积,三角形的面积公式即可得出结论.
解:S△AME=ACAN﹣![]() ANMN﹣
ANMN﹣![]() ACCE﹣
ACCE﹣![]() EFMF.
EFMF.
∵AB=n,BC=1,四边形ABMN及四边形BCEF均为正方形,
∴AN=MN=AB=n,EF=CE=BC=1,MF=BM﹣BF=n﹣1.
∴Sn=n(n+1)﹣![]() nn﹣
nn﹣![]() (n+1)﹣
(n+1)﹣![]() (n﹣1)=
(n﹣1)=![]() n2.
n2.
故答案为:![]() n2
n2
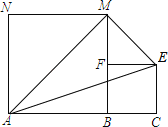

练习册系列答案
相关题目