��Ŀ����
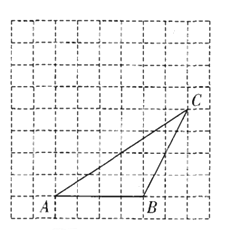
����Ŀ��С����С��������ɫ��Ϸ����ͼ��������������ת����ת�̣�ÿ��ת�̱��ֳ������ȵļ������Σ���Ϳ��ͼ����ʾ����ɫ��ͬʱת������ת�̣����ת��Aת���˺�ɫ��ת��Bת������ɫ������ת��Aת������ɫ��ת��Bת���˺�ɫ�����ɫ����ɫ��һ�������ɫ��

��1�������б�����״ͼ�ķ�����ʾ����Ϸ���п��ܳ��ֵĽ����
��2����������ɫ����С��ʤ������Ϸ�Ĺ����С����С����ƽ����˵�����ɣ�
���𰸡���1������������2������ƽ�������ɼ�����
��������
�����������1���������⣬���б��������п��ܳ��ֵĽ�������ɵô𰸣�
��2���ɣ�1���ı��������ܵõ���ɫ�ĸ��ʣ��õ����ۣ�
�⣺��1�����б��������п��ܳ��ֵĽ����ʾ���£����п��ܳ��ֵĽ������12�֣�
�� | ���죬�죩 | �������죩 | ���ƣ��죩 |
�� | ���죬���� | ���������� | ���ƣ����� |
�� | ���죬�죩 | �������죩 | ���ƣ��죩 |
�� | ���죬�ƣ� | �������ƣ� | ���ƣ��ƣ� |
�� | �� | �� |
��2������ȿ��ܳ��ֵ�12�ֽ���У���3��������ܵõ���ɫ���������ɫ�ĸ�����![]() =
=![]() ��
��
��С����ʤ�ĸ�����![]() ����С����ʤ�ĸ�����
����С����ʤ�ĸ�����![]() ��
��
��![]() ��
��![]() ��
��
��С����ʤ�Ŀ����Դ��������ɫ����Ϸ��˫���Dz���ƽ�ģ�