题目内容
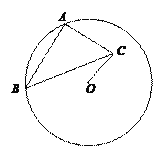
【题目】如果点
将
的弦
和
分成的四条线段
，
，
，
的长度恰好是四个互不相同的正整数，则称点为的”整分点”．现已知
是半径为
的上一点，则在半径
上有________个不同的整分点．
【答案】
【解析】
设PAPB=PCPD=k，则只需k不是质数和质数的平方，又有圆幂定理及⊙O的半径为5，得k=25-OP2，则k是小于25且不是质数和质数的平方的正整数弧，进而求得k的取值．从而得出满足题意的答案．
由已知得，线段PA，PB，PC，PD的长是互不相同的正整数，且满足PAPB=PCPD，
设PAPB=PCPD=k，则只需k不是质数和质数的平方即可，
又有圆幂定理及⊙O的半径为5，得k=25-OP2，
所以k是小于25且不是质数和质数的平方的正整数弧，
即k可以取6，8，10，12，14，15，16，18，20，21，22，24，共12个数．
故满足题意的整分点P，共有12个，但注意到弦长不大于直径，故满足题意的只有6，8，
即共有2个点．
故答案是：2．
练习册系列答案
相关题目
