题目内容
【题目】如图,在平面直角坐标系中,点A在第二象限,以A为顶点的抛物线经过原点,与x轴负半轴交于点B,对称轴为直线x=﹣1,点C在抛物线上,且位于点A、B之间(C不与A、B重合).若△ABC的周长为m,四边形AOBC的周长为 (用含m的式子表示).
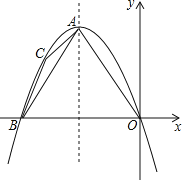
【答案】m+2.
【解析】
试题分析:根据抛物线的对称性得到:OB=2,AB=AO,则四边形AOBC的周长为AO+AC+BC+OB=△ABC的周长+OB,由此得出答案即可.
解:如图,
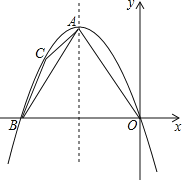
∵对称轴为直线x=﹣1,抛物线经过原点、x轴负半轴交于点B,
∴OB=2,
∵由抛物线的对称性知AB=AO,
∴四边形AOBC的周长为AO+AC+BC+OB=△ABC的周长+OB=m+2.
故答案为:m+2.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目