题目内容
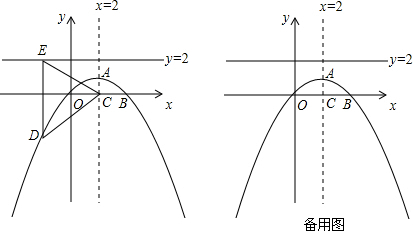
(2012•抚顺)如图,抛物线的对称轴是直线x=2,顶点A的纵坐标为1,点B(4,0)在此抛物线上.
(1)求此抛物线的解析式;
(2)若此抛物线对称轴与x轴交点为C,点D(x,y)为抛物线上一动点,过点D作直线y=2的垂线,垂足为E.
①用含y的代数式表示CD2,并猜想CD2与DE2之间的数量关系,请给出证明;
②在此抛物线上是否存在点D,使∠EDC=120°?如果存在,请直接写出D点坐标;如果不存在,请说明理由.

(1)求此抛物线的解析式;
(2)若此抛物线对称轴与x轴交点为C,点D(x,y)为抛物线上一动点,过点D作直线y=2的垂线,垂足为E.
①用含y的代数式表示CD2,并猜想CD2与DE2之间的数量关系,请给出证明;
②在此抛物线上是否存在点D,使∠EDC=120°?如果存在,请直接写出D点坐标;如果不存在,请说明理由.
分析:(1)已知抛物线的顶点坐标,可以将抛物线的解析式设为顶点式,再代入B点的坐标求解即可.
(2)①由坐标系两点间的距离公式不难得到CD2和DE2的表达式,再将(1)的抛物线解析式代入CD2的表达式中,用y替换掉x后,比较两者的大小关系即可;
②∠EDC是钝角,那么点D一定在x轴的上方,且抛物线对称轴的左右两侧各一个(它们关于抛物线对称轴对称),延长ED交x轴于F,在Rt△CDF中,∠DCF=30°,那么DC=2DF、CF=
DF,设出DF的长后,可以表示出CD、DE的长,由EF=ED+DF=2即可得出DF的长,从而求出点D的坐标.
(2)①由坐标系两点间的距离公式不难得到CD2和DE2的表达式,再将(1)的抛物线解析式代入CD2的表达式中,用y替换掉x后,比较两者的大小关系即可;
②∠EDC是钝角,那么点D一定在x轴的上方,且抛物线对称轴的左右两侧各一个(它们关于抛物线对称轴对称),延长ED交x轴于F,在Rt△CDF中,∠DCF=30°,那么DC=2DF、CF=
| 3 |
解答:解:(1)依题意,设抛物线的解析式为:y=a(x-2)2+1,代入B(4,0),得:
a(4-2)2+1=0,解得:a=-
∴抛物线的解析式:y=-
(x-2)2+1.
(2)①猜想:CD2=DE2;
证明:由D(x,y)、C(2,0)、E(x,2)知:
CD2=(x-2)2+y2,DE2=(y-2)2;
由(1)知:(x-2)2=-4(y-1)=-4y+4,代入CD2中,得:
CD2=y2-4y+4=(y-2)2=DE2.
 ②由于∠EDC=120°>90°,所以点D必在x轴上方,且抛物线对称轴左右两侧各有一个,以左侧为例:
②由于∠EDC=120°>90°,所以点D必在x轴上方,且抛物线对称轴左右两侧各有一个,以左侧为例:
延长ED交x轴于F,则EF⊥x轴;
在Rt△CDF中,∠FDC=180°-120°=60°,∠DCF=30°,则:
CD=2DF、CF=
DF;
设DF=m,则:CF=
m、CD=DE=2m;
∵EF=ED+DF=2m+m=2,
∴m=
,DF=m=
,CF=
m=
,OF=OC-CF=2-
,
∴D(2-
,
);
同理,抛物线对称轴右侧有:D(2+
,
);
综上,存在符合条件的D点,且坐标为(2-
,
)或(2+
,
).
a(4-2)2+1=0,解得:a=-
| 1 |
| 4 |
∴抛物线的解析式:y=-
| 1 |
| 4 |
(2)①猜想:CD2=DE2;
证明:由D(x,y)、C(2,0)、E(x,2)知:
CD2=(x-2)2+y2,DE2=(y-2)2;
由(1)知:(x-2)2=-4(y-1)=-4y+4,代入CD2中,得:
CD2=y2-4y+4=(y-2)2=DE2.
 ②由于∠EDC=120°>90°,所以点D必在x轴上方,且抛物线对称轴左右两侧各有一个,以左侧为例:
②由于∠EDC=120°>90°,所以点D必在x轴上方,且抛物线对称轴左右两侧各有一个,以左侧为例:延长ED交x轴于F,则EF⊥x轴;
在Rt△CDF中,∠FDC=180°-120°=60°,∠DCF=30°,则:
CD=2DF、CF=
| 3 |
设DF=m,则:CF=
| 3 |
∵EF=ED+DF=2m+m=2,
∴m=
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
∴D(2-
2
| ||
| 3 |
| 2 |
| 3 |
同理,抛物线对称轴右侧有:D(2+
2
| ||
| 3 |
| 2 |
| 3 |
综上,存在符合条件的D点,且坐标为(2-
2
| ||
| 3 |
| 2 |
| 3 |
2
| ||
| 3 |
| 2 |
| 3 |
点评:此题主要考查了抛物线解析式的确定、坐标系两点间的距离公式、解直角三角形等重要知识;(2)题中,由于①题为②题做了铺垫使得总体的难度降低了不少,最后一题中,一定要注意所求点的位置可能有多种情况.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 (2012•抚顺)如图,是五个相同的小正方体搭成的几何体,其主视图是( )
(2012•抚顺)如图,是五个相同的小正方体搭成的几何体,其主视图是( ) (2012•抚顺)如图,过点P(2,3)分别作PC⊥x轴于点C,PD⊥y轴于点D,PC、PD分别交反比例函数y=
(2012•抚顺)如图,过点P(2,3)分别作PC⊥x轴于点C,PD⊥y轴于点D,PC、PD分别交反比例函数y=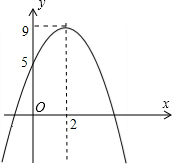 (2012•抚顺)如图,小浩从二次函数y=ax2+bx+c(a≠0)的图象中得到如下信息:
(2012•抚顺)如图,小浩从二次函数y=ax2+bx+c(a≠0)的图象中得到如下信息: (2012•抚顺)如图,已知一次函数y=-
(2012•抚顺)如图,已知一次函数y=-