题目内容
 (2012•抚顺)如图,已知一次函数y=-
(2012•抚顺)如图,已知一次函数y=-| 1 |
| 2 |
(1)求此一次函数的解析式;
(2)设点P为直线y=-
| 1 |
| 2 |
| 5 |
| 4 |
分析:(1)直接把点A(2,3)代入一次函数y=-
x+b即可求出b的值,进而得出一次函数的解析式;
(2)设P(p,d),p>0,再根据点P在一次函数的图象上及S△POQ=
S△AOB,即可得出关于p、d的方程组,求出p、d的值即可.
| 1 |
| 2 |
(2)设P(p,d),p>0,再根据点P在一次函数的图象上及S△POQ=
| 5 |
| 4 |
解答:解:(1)∵一次函数y=-
x+b的图象经过点A(2,3),
∴3=(-
)×2+b,
解得b=4,
故此一次函数的解析式为:y=-
x+4;
(2)设P(p,d),p>0,
∵点P在直线y=-
x+4的图象上,
∴d=-
p+4①,
∵S△POQ=
S△AOB=
×
×2×3,
∴
pd=
②,
①②联立得,
,
解得
或
,
∴P点坐标为:(3,
)或(5,
).
| 1 |
| 2 |
∴3=(-
| 1 |
| 2 |
解得b=4,
故此一次函数的解析式为:y=-
| 1 |
| 2 |
(2)设P(p,d),p>0,
∵点P在直线y=-
| 1 |
| 2 |
∴d=-
| 1 |
| 2 |
∵S△POQ=
| 5 |
| 4 |
| 5 |
| 4 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 15 |
| 4 |
①②联立得,
|
解得
|
|
∴P点坐标为:(3,
| 5 |
| 2 |
| 3 |
| 2 |
点评:本题考查的是用待定系数法求一次函数的解析式及一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目

 (2012•抚顺)如图,是五个相同的小正方体搭成的几何体,其主视图是( )
(2012•抚顺)如图,是五个相同的小正方体搭成的几何体,其主视图是( ) (2012•抚顺)如图,过点P(2,3)分别作PC⊥x轴于点C,PD⊥y轴于点D,PC、PD分别交反比例函数y=
(2012•抚顺)如图,过点P(2,3)分别作PC⊥x轴于点C,PD⊥y轴于点D,PC、PD分别交反比例函数y=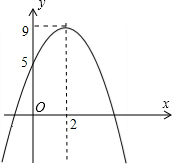 (2012•抚顺)如图,小浩从二次函数y=ax2+bx+c(a≠0)的图象中得到如下信息:
(2012•抚顺)如图,小浩从二次函数y=ax2+bx+c(a≠0)的图象中得到如下信息: