Question

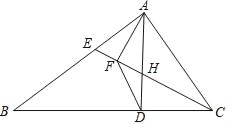
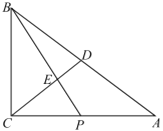
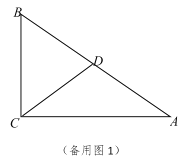
【题目】在△ABC中，∠ACB=90°，点E是斜边AB的中点，AB=10，BC=8，点P在CE的延长线上，过点P作PQ⊥CB，交CB的延长线于点Q，设EP=x

（1）如图1，求证：△ABC∽△PCQ；

（2）如图2，连接PB，当PB平分∠CPQ时，试用含x的代数式表示△PBE的面积；

（3）如图3，过点B作BF⊥AB交PQ于点F．若∠BEF=∠A，试求x的值．

Answer 1

【答案】（1）证明见解析；（2）；（3）x=10．

【解析】

（1）易证明到∠PQC=∠ACB．即可求证：△ABC∽△PCQ

（2）过点B作BH⊥PC于H，可证BH=BQ，此时根据（1）中：△ABC∽△PCQ，可解得BQ=BH=，即可求解．

（3）已知BC=8，AB=10，通过证明△ABC∽△BFQ，求出BF，再证△ACB∽△EBF，可得，即可求出x的值．

解：（1）∵点E是斜边AB的中点，

∴CE=，

∴∠PCQ=∠ABC

∵PQ⊥CB

∴∠PQC=90°

又∵∠ACB=90°，

∴∠PQC=∠ACB

∴△ABC∽△PCQ

（2）过点B作BH⊥PC于H，

∵BP平分∠CPQ，BH⊥PC，BQ⊥PQ

∴BH=BQ

由（1）知，△ABC∽△PCQ，

∴，即AB×CQ=BC×PC

而AB=10，BC=8，CQ=BC+BQ=8+BQ，PC=CE+EP=5+x

∴10×（8+BQ）=8×（5+x），解得BQ=，

∴BH=

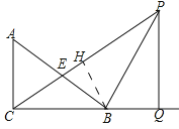
（3）∵∠FBQ+∠ABC=90°，∠A+∠ABC=90°

∴∠A=∠FBQ

又∵∠ACB=∠EBF=90°，

∴△ABC∽△BFQ

∴，即AB×BQ=AC×BF

又由（2）知BQ=

∴=6×BF，解得BF=

∵∠FEB=∠A，∠EBF=∠ACB=90°

∴△ACB∽△EBF

∴，即

解得x=10