题目内容
【题目】如图,正方形ABCD的边长为4,点E是CD的中点,AF平分∠BAE交BC于点F,将△ADE绕点A顺时针旋转90°得△ABG,则CF的长为____.
【答案】6﹣2![]() .
.
【解析】
作FM⊥AD于M, FN⊥AG于N,如图,易得四边形CFMD为矩形,则FM=4,利用勾股定理计算出AE=![]() ,再根据旋转的性质得到AG=AE=2
,再根据旋转的性质得到AG=AE=2![]() ., BG=DE=2,∠1=∠4,∠GAE=90°,∠ABG=∠D=90°,于是可判断点G、 C、B三点共线,接着证明FA平分∠GAD得到FN=FM=4,然后利用等面积法计算出GF,从而计算CG-GF就可得到CF的长.
., BG=DE=2,∠1=∠4,∠GAE=90°,∠ABG=∠D=90°,于是可判断点G、 C、B三点共线,接着证明FA平分∠GAD得到FN=FM=4,然后利用等面积法计算出GF,从而计算CG-GF就可得到CF的长.
解:作FM⊥AD于M, FN⊥AG于N,如图,
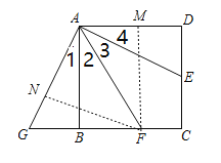
易得四边形CFMD为矩形,则FM=4,
∵正方形ABCD的边长为4,E是CD的中点,
∴DE=2,
∴AE=![]()
∵△ADE绕点A顺时针旋转90°得△ABG
∴AG=AE=![]() ,BG=DE=2,∠1=∠4,∠GAE=90°,∠ABG=∠D=90° ,
,BG=DE=2,∠1=∠4,∠GAE=90°,∠ABG=∠D=90° ,
而∠ABC=90°,
∴点G、C、B三点共线.
∴AF平分∠BAE交BC于点F,
∴∠2=∠3,
∴∠1+∠2=∠3+∠4
∴∠GAF=∠FAD,
∴FA平分∠GAD,
∴FN=FM=4,
∴![]()
∴GF=![]()
.CF=CG-GF=4+2-![]() =6-
=6-![]()

练习册系列答案
相关题目