题目内容
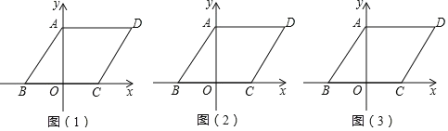
【题目】如图,平面直角坐标系中,函数y=![]() 的图像与x、y轴分别交于点A、B.以AB为直径作
的图像与x、y轴分别交于点A、B.以AB为直径作![]() M.
M.

(1)求AB的长;
(2)点D是![]() M上任意一点,且点D在直线AB上方,过点D作DH⊥AB,垂足为H,连接BD.
M上任意一点,且点D在直线AB上方,过点D作DH⊥AB,垂足为H,连接BD.
①当△BDH中有一个角等于![]() BAO两倍时,求点D的坐标;
BAO两倍时,求点D的坐标;
②当![]() DBH=45°时,求点D的坐标.
DBH=45°时,求点D的坐标.
【答案】(1)AB=4;(2)①(![]() ,3);D(-2
,3);D(-2![]() );②D(
);②D(![]() ).
).
【解析】
(1)根据一次函数的解析式求出A,B两点的坐标,再利用勾股定理即可求出AB的长;(2)①连接OM,由OM为Rt△AOB斜边AB上中线,证得△OBM为等边三角形,则∠OBM=60°,得到∠BAO=30°,再分∠DBH=2∠BAO=60°时与∠BDH=2∠BAO=60°时两种情况分别讨论求解;②当∠DBH=45°时,易得∠DAB=45°,则AH=DH=BH,所以M、H重合,作DC⊥y轴于C,DE⊥x轴于E,易证△DCB≌△DEA,得CB=AE,设CB=AE=a,则DC=OE=2![]() ,因为BD=
,因为BD=![]() ,由勾股定理得,DC2+CB2=DB2,所以
,由勾股定理得,DC2+CB2=DB2,所以![]() ,求出a的值,再根据题意舍去一个,即可求解.
,求出a的值,再根据题意舍去一个,即可求解.
解:(1)对于y=![]() ,
,
当x=0时,y=2;当y=0时,x=-2![]() .
.
所以点A(-2![]() ,B(0,2),
,B(0,2),
所以OB=2,OA=2![]() .根据勾股定理得,AB=
.根据勾股定理得,AB=![]() =4.
=4.
(2)①连接OM.
因为OM为Rt△AOB斜边AB上中线,
所以OM=AM=BM=![]() AB=2=OB,
AB=2=OB,
所以△OBM为等边三角形,则∠OBM=60°,
故∠BAO=30°.
1)如图,当∠DBH=2∠BAO=60°时,
连接DM,并延长交AO于点N.
∵∠DBH=60°,DM=BM,
∴△BDM为等边三角形,
∴∠DMB =60°,
故∠AMN=∠DMB =60°,
所以∠MNA=180-30°-60°=90°,
所以MN⊥AO,即DN⊥AO,
∴ON=![]() AO=
AO=![]()
DN=DM+MN=BM+![]() AM=
AM=![]() AB+
AB+![]() AB=3,
AB=3,
所以D(![]() ,3);
,3);
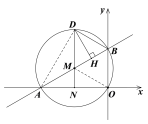
2)如图,
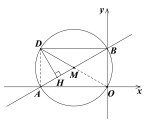
当∠BDH=2∠BAO=60°时,
∵DM=BM=AM=OM,
∴四边形BDAO为矩形,
可得,DA=BO=2,BD=OA=2![]() .
.
所以D(-2![]() ).
).
②如图,
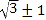
当∠DBH=45°时,
∵AH=BH,DM⊥AB,∴△ABD为等腰直角三角形,
∴∠DAB=45°,
则AH=DH=BH,所以M、H重合.
作DC⊥y轴于C,DE⊥x轴于E,
∵DE⊥AO,DC⊥CO,
∴∠ADE+∠EDB=90°,又∠EDB+∠BDC=90°,
∴∠ADE=∠BDC
又AD=BD,
∴△DCB≌△DEA(AAS),得CB=AE,
设CB=AE=a,则DC=OE=2![]() ,
,
因为BD=![]() ,
,
由勾股定理得,DC2+CB2=DB2,
所以![]() ,
,
解得a=![]() ,
,
当a=![]() 时,OC=DE=3+
时,OC=DE=3+![]() >4,不符合题意.
>4,不符合题意.
当a=![]() 时,OC=OE=
时,OC=OE=![]() ,所以D(
,所以D(![]() )
)