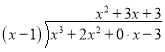��Ŀ����
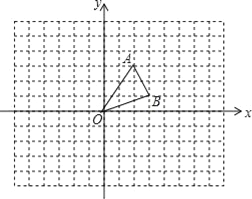
����Ŀ����ƽ��ֱ������ϵ�У���ABO��������������ֱ�Ϊ��A��2��3����B��3��1����O��0��0����
��1������ABO����ƽ��4����λ������ƽ�ƺ�ġ�A1B1O1��
��2������ABO�Ƶ�O˳ʱ����ת180�㣬������ת��õ��ġ�A2B2O����ʱ�ı���ABA2B2����״��������
��3����ƽ�����Ƿ���ڵ�D��ʹ����A��B��O��DΪ������ı�����ƽ���ı��Σ���������ֱ��д���������������е�����ꣻ�������ڣ���˵�����ɣ�
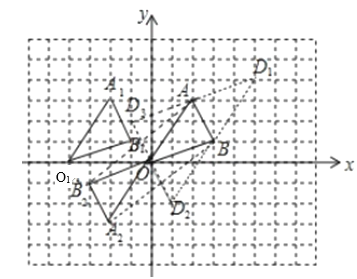
���𰸡���1��ͼ�μ�������2��ƽ���ı��Σ�3������1��2������1����2������5��4��
��������
��1�����õ�ƽ�Ƶ��������д����A��B��Oƽ�ƺ�Ķ�Ӧ��A1��B1��C1��Ȼ����㼴�ɵõ���A1B1O1��
��2�����ù���ԭ��ԳƵĵ����������д��A2��B2�����꣬���ɵõ���A2B2O�����öԽ�����ƽ�ֵ��ı���Ϊƽ���ı��ο��ж��ı���ABA2B2����״��
��3���������ۣ��ֱ���AB��BO��AOΪ�Խ���ƽ���ı��οɵõ����������ĵ�D��Ȼ��д����Ӧ��D�����꣮
(1)��ͼ,��A1B1O1Ϊ������
(2)��ͼ,��A2B2OΪ����,��ʱ�ı���ABA2B2����״��ƽ���ı���.�ʴ�Ϊƽ���ı��Σ�
(3)����.��ͼ���������ĵ�D������Ϊ(5,4)��(1,2)��(1,2)

 ����������ϵ�д�
����������ϵ�д� �Ż���ҵ�Ϻ��Ƽ����׳�����ϵ�д�
�Ż���ҵ�Ϻ��Ƽ����׳�����ϵ�д�