Question

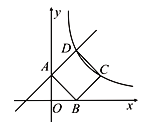
【题目】如图，一次函数的图象与轴交于点A，正方形ABCD的顶点B在轴上，点D在直线上，且AO=OB，反比例函数（）经过点C．

（1）求一次函数和反比例函数的解析式；

（2）点P是轴上一动点，当的周长最小时，求出P点的坐标；

（3）在（2）的条件下，以点C、D、P为顶点作平行四边形，直接写出第四个顶点M的坐标．

Answer 1

【答案】（1）y=x+2，；（2）P（，0）；（3）M的坐标为（，2），（，6）或（，﹣2）．

【解析】

（1）设一次函数y=kx+2的图象与x轴交于点E，连接BD，利用一次函数图象上点的坐标特征、正方形的性质以及等腰三角形的性质可得出点E的坐标，由点E的坐标利用待定系数法可求出一次函数解析式，由BD∥OA，OE=OB可求出BD的长，进而可得出点D的坐标，由正方形的性质可求出点C的坐标，再利用反比例函数图象上点的坐标特征可求出反比例函数解析式；

（2）作点D关于x轴的对称点D'，连接CD'交x轴于点P，此时△PCD的周长取最小值，由点D的坐标可得出点D'的坐标，由点C，D'的坐标，利用待定系数法可求出直线CD'的解析式，再利用一次函数图象上点的坐标特征可求出点P的坐标；

（3）设点M的坐标为（x，y），分DP为对角线、CD为对角线及CP为对角线三种情况，利用平行四边形的性质（对角线互相平分）可求出点M的坐标，此题得解．

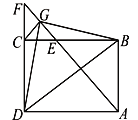
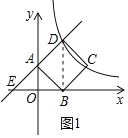
（1）设一次函数y=kx+2的图象与x轴交于点E，连接BD，如图1所示．

当x=0时，y=kx+2=2，∴OA=2．

∵四边形ABCD为正方形，OA=OB，∴∠BAE=90°，∠OAB=∠OBA=45°，∴∠OAE=∠OEA=45°，∴OE=OA=2，点E的坐标为（﹣2，0）．

将E（﹣2，0）代入y=kx+2，得：﹣2k+2=0，解得：k=1，∴一次函数的解析式为y=x+2．

∵∠OBD=∠ABD+∠OBA=90°，∴BD∥OA．

∵OE=OB=2，∴BD=2OA=4，∴点D的坐标为（2，4）．

∵四边形ABCD为正方形，∴点C的坐标为（2+2﹣0，0+4﹣2），即（4，2）．

∵反比例函数y（x＞0）经过点C，∴n=4×2=8，∴反比例函数解析式为y．

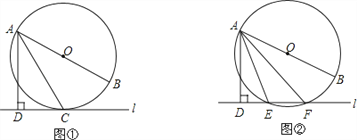
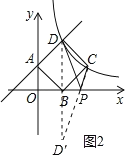
（2）作点D关于x轴的对称点D'，连接CD'交x轴于点P，此时△PCD的周长取最小值，如图2所示．

∵点D的坐标为（2，4），∴点D'的坐标为（2，﹣4）．

设直线CD'的解析式为y=ax+b（a≠0），将C（4，2），D'（2，﹣4）代入y=ax+b，得：，解得：，∴直线CD'的解析式为y=3x﹣10．

当y=0时，3x﹣10=0，解得：x，∴当△PCD的周长最小时，P点的坐标为（，0）．

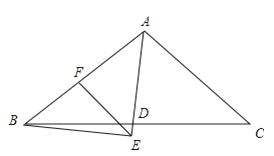
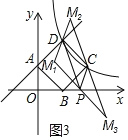
（3）设点M的坐标为（x，y），分三种情况考虑，如图3所示．

①当DP为对角线时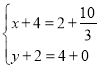，，解得：，∴点M1的坐标为（，2）；

②当CD为对角线时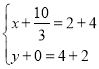，，解得：，∴点M2的坐标为（，6）；

③当CP为对角线时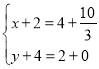，，解得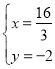：，∴点M3的坐标为（，﹣2）．

综上所述：以点C、D、P为顶点作平行四边形，第四个顶点M的坐标为（，2），（，6）或（，﹣2）．