题目内容
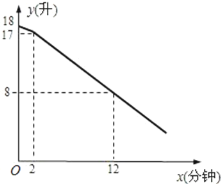
【题目】教室里放有一台饮水机(如图),饮水机上有两个放水管.课间同学们依次到饮水机前用茶杯接水.假设接水过程中水不发生泼洒,每个同学所接的水量都是相等的.两个放水管同时打开时,它们的流量相同.放水时先打开一个水管,过一会儿,再打开第二个水管,放水过程中阀门一直开着.饮水机的存水量y(升)与放水时间x(分钟)的函数关系如图所示:
(1)求出饮水机的存水量y(升)与放水时间x(分钟)(x≥2)的函数关系式;
(2)如果打开第一个水管后,2分钟时恰好有4个同学接水结束,则前22个同学接水结束共需要几分钟?
(3)按(2)的放法,求出在课间10分钟内班级中最多有多少个同学能及时接完水?

【答案】(1)y=-![]() x+
x+![]() (2≤x≤
(2≤x≤![]() );(2)前22个同学接水共需7分钟;(3)课间10分钟最多有32人及时接完水.
);(2)前22个同学接水共需7分钟;(3)课间10分钟最多有32人及时接完水.
【解析】
(1)设函数解析式为y=kx+b(k≠0),由图象可知直线过点(2,17)、(12,8),代入函数解析式求解k、b的值即可;
(2)要求得前22位同学接水所用的时间,可根据存水量与放水时间的函数关系式来解答,即需先求出每个同学接水量;结合以上所求得的信息,即可求出前22位同学接完水后的余水量,将其代入以上求得的函数关系式中,即可求得所用的时间;
(3)同理,根据第二问的解题思路,先根据函数关系式求出课间10分钟存水量,从而可得到最多有多少同学能及时接完水.
(1)设存水量y与放水时间x的解析式为y=kx+b
把(2,17)、(12,8)代入y=kx+b得
![]() 解得k=-
解得k=-![]() ,b=
,b=![]()
y=-![]() x+
x+![]() (2≤x≤
(2≤x≤![]() )
)
(2)由图可得每个同学接水量是0.25升,则前22个同学需接水0.25×22=5.5升
存水量y=18-5.5=12.5升 ∴12.5=-![]() x+
x+![]() ∴x=7
∴x=7
∴前22个同学接水共需7分钟.
(3)当x=10时存水量y=-![]() ×10+
×10+![]() =
=![]()
用去水18-![]() =8.2升 8.2÷0.25=32.8
=8.2升 8.2÷0.25=32.8
∴课间10分钟最多有32人及时接完水.

【题目】综合与实践
元且期间,我市各大商场掀起购物狂湖,现有甲、乙、丙三个商场开展的促销活动如表所示:
商场 | 优惠活动 |
甲 | 全场按标价的 |
乙 | 实行“满 (如:顾客购衣服 |
丙 | 实行“满 |
根据以上活动信息,解决以下问题:
(1)三个 商场同时出售一件标价![]() 元的上衣和一条标价
元的上衣和一条标价![]() 元的裤子,王阿姨想买这一套衣服,她应该选择哪家商场更划算?
元的裤子,王阿姨想买这一套衣服,她应该选择哪家商场更划算?
(2)黄 先生发现在甲、乙商场同时出售一件标价![]() 元的上衣和一条标价
元的上衣和一条标价![]() 多元的裤子,最后付款也一样,诸问这条裤子的标价是多少元?
多元的裤子,最后付款也一样,诸问这条裤子的标价是多少元?
(3)丙商场又推出 “先打折”,“再满![]() 减
减![]() 元”的活动,张先生买了一件标价为
元”的活动,张先生买了一件标价为![]() 元的上衣,张先生发现竟然比没打折前多付了
元的上衣,张先生发现竟然比没打折前多付了![]() 元钱,问丙商场先打了多少折后再参加活动?
元钱,问丙商场先打了多少折后再参加活动?