题目内容
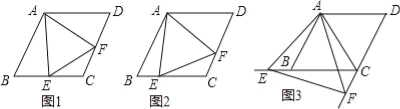
【题目】如图,在△ABC中,AD平分∠BAC,BE⊥AD,BE交AD的延长线于点E,点F在AB上,且EF∥AC.求证:点F是AB的中点.
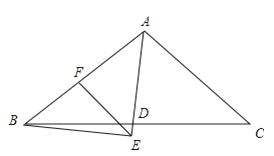
【答案】详见解析.
【解析】
由AD为角平分线可得再由∠BAE=∠CAE,由EF∥AC,根据两直线平行内错角相等可得∠AEF=∠CAE,所以∠AEF=∠BAE,根据等角对等边即可得AF=EF.又因∠BAE+∠ABE=90°,∠BEF+∠AEF=90°,∠AEF=∠BAE,利用等角的余角相等可得出∠BEF=∠ABE,根据等角对等边得到即可得BF=EF,所以AF=BF,即F为AB的中点.
证明:∵AD平分∠BAC,
∴∠BAE=∠CAE,
∵EF∥AC,
∴∠AEF=∠CAE,
∴∠AEF=∠BAE,
∴AF=EF,
又∵BE⊥AD,
∴∠BAE+∠ABE=90°,∠BEF+∠AEF=90°,
又∠AEF=∠BAE,
∴∠ABE=∠BEF,
∴BF=EF,
∴AF=BF,
∴F为AB中点.

练习册系列答案
相关题目