题目内容
【题目】如图，已知直线y=﹣x+4与反比例函数y= 
的图象相交于点A（﹣2，a），并且与x轴相交于点B．
（1）求反比例函数的表达式；
（2）求△AOB的面积．
【答案】
（1）解：将A（﹣2，a）代入y=﹣x+4中，
得：a=﹣（﹣2）+4=6，
∴A点坐标（﹣2，6），
将A（﹣2，6）代入 
中，
得： 
，即k=﹣12，
所以反比例函数表达式为： 
（2）解：如图，过A点作AD⊥x轴于D，
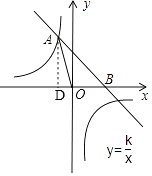
因为 A（﹣2，6），
所以AD=6，
在直线y=﹣x+4中，令y=0，得x=4，
所以 B（4，0）即OB=4，
所以S△AOB= 
OB×AD= ×4×6=12
【解析】（1）把A点坐标代入直线解析式，求出a，再代入双曲线解析式即可求出k ;（2）须作出OB边上的高，利用面积公式S△AOB= OB×AD可求出结果.
练习册系列答案
相关题目
