题目内容
【题目】如图1，矩形OABC的两条边OA、OC分别在y轴和x轴上，已知点A（0，3）、点C（－4，0）．
（1）若把矩形OABC沿直线DE折叠，使点C落在点A处，直线DE与OC、AC、AB的交点分别为D、F、E，求折痕DE的长；
（2）若点P在x轴上，在平面内是否存在点Q，使以P、D、E、Q为顶点的四边形是菱形？若存在，则请直接写出点Q的坐标；若不存在，请说明理由；
（3）如图2，若M为AC边上的一动点，在OA上取一点N（0，1），将矩形OABC绕点O顺时针旋转一周，在旋转的过程中，M的对应点为M1，请直接写出NM1的最大值和最小值．
【答案】（1）
；（2）当DE是菱形的对角线时，Q1（0，3），当DE是菱形的边时，Q2（
，3），Q3（－
，3），Q4（－
，－3）；（3）最大值是5，最小值是
．
【解析】
（1）由△DFC∽△AOC，求出DF，再证明EF=DF；
（2）分两种情形分别讨论即可：①DE为菱形的边．②DE为菱形的对角线；
（3）由题意点M在如图3中的圆环内或两个圆上，利用图象法即可解决问题；
解：（1）解：（1）∵四边形OABC是矩形，
∴∠AOC=90°．
∵OA=3，OC=4，
∴AC=5．
由折叠可得：
∵∠FCD=∠OCA，∠DFC=∠AOC=90°，
∴△DFC∽△AOC．
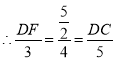
∵四边形OABC是矩形，
∴AB∥DC，
∴∠EAF=∠DCF
∴△AFE≌△CFD（ASA）．
∴EF=DF．
∴折痕DE的长为
（2）如下图，由（1）可知，
当DE为菱形的边时，
，可得
；
当DE为菱形的对角线时，P与C重合，Q与A重合，Q2（0，3），
当点Q在第四象限，E与Q关于x轴对称，
综上所述，满足条件的点Q坐标为
或
或（0，3）或
；
（3）如图3中，作OH⊥AC，则
观察图形可知，MN的最小值=OM-ON 
；
MN的最大值=NM′=ON+OM′=1+4=5
