题目内容
【题目】在![]() O中,弦AB和弦AC构成的∠BAC=28°,M、N分别是AB和AC的中点,则∠MON的度数为______.
O中,弦AB和弦AC构成的∠BAC=28°,M、N分别是AB和AC的中点,则∠MON的度数为______.
【答案】28°或152°
【解析】
连接OM,ON,利用垂径定理得OM⊥AB,ON⊥AC,再分类讨论,当AB,AC在圆心异侧时(如图1),利用四边形内角和得结果;当AB,AC在圆心同侧时(如图2),利用相似三角形的性质得结果.
连接OM,ON,
∵M、N分别是AB和AC的中点,
∴OM⊥AB,ON⊥AC,
OM⊥AB,ON⊥AC,
当AB,AC在圆心异侧时(如图1),
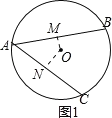
∵∠BAC=28°,
在四边形AMON中,
∴∠MON=360°﹣90°﹣90°﹣28°=152°;
当AB,AC在圆心同侧时(如图2),
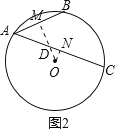
∵∠ADM=∠ODN,∠AMD=∠OND,
∴△ADM∽△ODN,
∴∠MON=∠BAC=28°.
故答案为:152°或28°.

练习册系列答案
相关题目