Question

如图，平面直角坐标系的单位是厘米，直线AB的解析式为y=

3

x-6

3

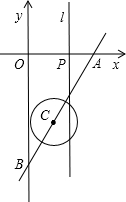，分别与x轴y轴相交于A、B两点．点C在射线BA上以3cm/秒的速度运动，以C点为圆心作半径为1cm的⊙C．点P以2cm/秒的速度在线段OA上来回运动，过点P作直线l垂直与x轴．
（1）求A、B两点的坐标；
（2）若点C与点P同时从点B、点O开始运动，求直线l与⊙C第2次相切时点P的坐标；
（3）在整个运动过程中，直线l与⊙C有交点的时间共有多少秒？

Answer 1

分析：（1）根据直线方程分别令x，y值为零，即可得出B，A坐标．
（2）先求出第二次相切的时间，然后算出BC长度，最终得到C点坐标．
（3）直线与圆第二次相交共有两次，分别算出两次的相交时间．

解答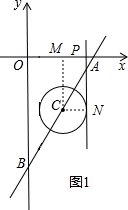：解：（1）由直线方程，令x=0得y=-6

3

则B点坐标为（0，-6

3

）；
令y=0得x=6则A点坐标为（6，0）．

（2）如图1，直线l与⊙C第2次相切时，
根据题意得：12-2t=3t•cos60°+1，解得t=

22

7

，
则P点横坐标为3×

22

7

×cos60°+1=

40

7

，P点纵坐标为：0
则P点坐标为（

40

7

，0）；

（3）第一次有交点时间为T，则2T-3T×cos60°=1得，T=2，
第二次相交时间为S，则3S×cos60°+2S=2得，S=

4

7

，
则有交点的时间共2+

4

7

=2

4

7

秒．

点评：本题重点为分析出直线和圆何时相切，第一次相切在P向A运动的过程中，第二次相切是在P由A向O运行的工程中．相切是有交点的临界点．