题目内容
已知一次函数 的图象与反比例函数
的图象与反比例函数 的图象相交,其中一个交点的纵坐标为6.
的图象相交,其中一个交点的纵坐标为6.
(1)求两个函数的解析式;
(2)若已知另一点的横坐标为 ,结合图象求出
,结合图象求出 时x的取值范围.
时x的取值范围.
(1)y1=3x+10, ;(2)x<-2或
;(2)x<-2或 <x<0.
<x<0.
解析试题分析:(1)将给出的交点的纵坐标代入两个函数式中,得出两个关于k,x的方程,然后联立方程组,即可求出k的值,也就确定了两个函数的解析式;(2)根据图象和A、B的横坐标即可得出答案.
试题解析:(1)∵一个交点的纵坐标为6,∴ ,解得:k=-5.
,解得:k=-5.
∴一次函数解析式为y1=3x+10;反比例函数解析式为 .
.
(2)作出图象如图,
∵A的横坐标是-2,B的横坐标是 ,
,
∴y1<y2时x的取值范围x<-2或 <x<0.
<x<0.
考点:1.反比例函数与一次函数的交点问题;2.曲线上点的坐标与方程的关系;3.数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
一次函数y=kx+4的图象经过点(-3,-2),则
(1)求这个函数表达式;并画出该函数的图象.
(2)判断(-5,3)是否在此函数的图象上;
(3)求把这条直线沿x轴向右平移1个单位长度后的函数表达式.
漳州三宝之一“水仙花”畅销全球,某花农要将规格相同的800件水仙花运往A,B,C三地销售,要求运往C地的件数是运往A地件数的3倍,各地的运费如下表所示:
| | A地 | B地 | C地 |
| 运费(元/件) | 20 | 10 | 15 |
(2)若总运费不超过12000元,最多可运往A地的水仙花多少件?
 x的图象相交于点(4,a),求:
x的图象相交于点(4,a),求: 与直线
与直线 相交于点A(4,m)、B.
相交于点A(4,m)、B.
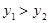 ?(直接写出答案)
?(直接写出答案) (小时)的一次函数.某天该汽车外出时,油箱中余油量与行驶时间的变化关系如图:
(小时)的一次函数.某天该汽车外出时,油箱中余油量与行驶时间的变化关系如图:
 与反比例函数
与反比例函数 的图象相交于点A,且点A的纵坐标为1.
的图象相交于点A,且点A的纵坐标为1.
 ,点C的坐标为(-18,0).
,点C的坐标为(-18,0).