题目内容
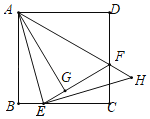
【题目】如图,矩形ABCD中,AB=10,AD=4,点E从D向C以每秒1个单位的速度运动,以AE为一边在AE的左上方作正方形AEFG,同时垂直于CD的直线MN也从C向D以每秒2个单位的速度运动,当点F落在直线MN上,设运动的时间为t,则t的值为( )

A.1B.![]() C.4D.
C.4D.![]()
【答案】D
【解析】
过点F作FH⊥CD,交直线CD于点Q,则∠EHF=90°,易证∠ADE=∠EHF,由正方形的性质得出∠AEF=90°,AE=EF,证得∠AED=∠EFH,由AAS证得△ADE≌△EHF得出AD=EH=4,则t+2t=4+10,即可得出结果.
过点F作FH⊥CD,交直线CD于点Q,则∠EHF=90°,如图所示:
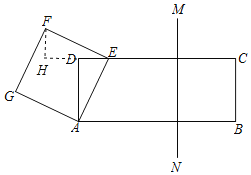
∵四边形ABCD为矩形,
∴∠ADE=90°,
∴∠ADE=∠EHF,
∵在正方形AEFG中,∠AEF=90°,AE=EF,
∴∠AED+∠HEF=90°,
∵∠HEF+∠EFH=90°,
∴∠AED=∠EFH,
在△ADE和△EHF中,
 ,
,
∴△ADE≌△EHF(AAS),
∴AD=EH=4,
由题意得:t+2t=4+10,
解得:t=![]() ,
,
故选D.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目