题目内容
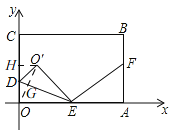
【题目】如图,在平面直角坐标系中,点B(12,10),过点B作x轴的垂线,垂足为A.作y轴的垂线,垂足为C.点D从O出发,沿y轴正方向以每秒1个单位长度运动;点E从O出发,沿x轴正方向以每秒3个单位长度运动;点F从B出发,沿BA方向以每秒2个单位长度运动.当点E运动到点A时,三点随之停止运动,运动过程中△ODE关于直线DE的对称图形是△O′DE,设运动时间为t.
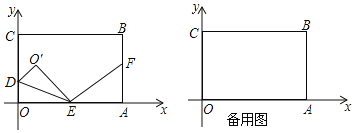
(1)用含t的代数式分别表示点E和点F的坐标;
(2)若△ODE与以点A,E,F为顶点的三角形相似,求t的值;
(3)当t=2时,求O′点在坐标.
【答案】(1)E(3t,0),F(12,10﹣2t);(2)t=![]() ;(3)O'(
;(3)O'(![]() ,
,![]() )
)
【解析】
(1)直接根据路程等于速度乘以时间,即可得出结论;
(2)先判断出∠DOE=∠EAF=90°,再分两种情况,用相似三角形得出比例式,建立方程求解,最后判断即可得出结论;
(3)先根据勾股定理求出DE,再利用三角形的面积求出OG,进而求出OO',再判断出△OHO'∽△EOD,得出比例式建立方程求解即可得出结论.
解:(1)∵BA⊥x轴,CB⊥y轴,B(12,10),
∴AB=10,
由运动知,OD=t,OE=3t,BF=2t(0≤t≤4),
∴AF=10﹣2t,
∴E(3t,0),F(12,10﹣2t);
(2)由(1)知,OD=t,OE=3t,AF=10﹣2t,
∴AE=12﹣3t,
∵BA⊥x轴,
∴∠OAB=90°=∠AOC,
∵△ODE与以点A,E,F为顶点的三角形相似,
∴△DOE∽△EAF或△DOE∽△FAE,
①当△DOE∽△EAF时,![]() ,
,
∴![]() ,
,
∴t=![]() ,
,
②当△DOE∽△FAE时,![]() ,
,
∴![]() ,
,
∴t=6(舍),
即:当△ODE与以点A,E,F为顶点的三角形相似时,t=![]() 秒;
秒;
(3)如图,
当t=2时,OD=2,OE=6,
在Rt△DOE中,根据勾股定理得,DE=2![]() ,
,
连接OO'交DE于G,
∴OO'=2OG,OO⊥DE,
∴S△DOE=![]() ODOE=
ODOE=![]() DEOG,
DEOG,
∴OG=![]() =
=![]() =
=![]() ,
,
∴OO'=2OG=![]() ,
,
∵∠AOC=90°,
∴∠HOO'+∠AOO'=90°,
∵OO'⊥DE,
∴∠OED+∠AOO'=90°,
∴∠HOO'=∠OED,
过点O'作O'H⊥y轴于H,
∴∠OHO'=90°=∠DOE,
∴△OHO'∽△EOD,
∴![]() ,
,
∴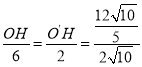 ,
,
∴OH=![]() ,O'H=
,O'H=![]() ,
,
∴O'(![]() ,
,![]() ).
).