题目内容
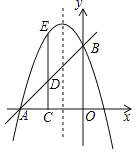
【题目】如图,已知抛物线![]() 与x轴交于点A、B,与y轴分别交于点C,其中点
与x轴交于点A、B,与y轴分别交于点C,其中点![]() ,点
,点![]() ,且
,且![]() .
.
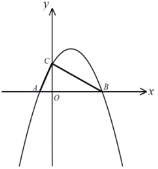
(1)求抛物线的解析式;
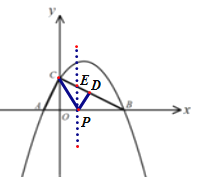
(2)点P是线段AB上一动点,过P作![]() 交BC于D,当
交BC于D,当![]() 面积最大时,求点P的坐标;
面积最大时,求点P的坐标;
(3)点M是位于线段BC上方的抛物线上一点,当![]() 恰好等于
恰好等于![]() 中的某个角时,求点M的坐标.
中的某个角时,求点M的坐标.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,S最大,此时
时,S最大,此时![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)先根据射影定理求出点![]() ,设抛物线的解析式为:
,设抛物线的解析式为:![]() ,将点
,将点![]() 代入求出
代入求出![]() ,然后化为一般式即可;
,然后化为一般式即可;
(2)过点P作y轴的平行线交BC于点E,设![]() ,用待定系数法分别求出直线BC,直线AC,直线PD的解析式,表示出点E,点D的坐标,然后根据三角形面积公式列出二次函数解析式,利用二次函数的性质求解即可;
,用待定系数法分别求出直线BC,直线AC,直线PD的解析式,表示出点E,点D的坐标,然后根据三角形面积公式列出二次函数解析式,利用二次函数的性质求解即可;
(3)分两种情况求解:当![]() 时和当
时和当![]() 时.
时.
(1)∵![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴由射影定理可得:![]() ,
,
∴![]() ,∴点
,∴点![]() ,
,
设抛物线的解析式为:![]() ,将点
,将点![]() 代入上式得:
代入上式得:![]() ,
,
∴抛物线的解析式为:![]() ;
;
(2)过点P作y轴的平行线交BC于点E,设![]() ,
,
设![]() ,
,
把![]() ,
,![]() 代入得
代入得
![]() ,
,
∴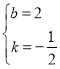 ,
,
∴![]() ,
,
∴![]() ,
,
同样的方法可求![]() ,
,
故可设![]() ,把
,把![]() 代入得
代入得![]() ,
,
联立 解得:
解得: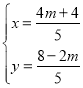 ,
,
∴![]() ,
,
![]() ,
,
故当![]() 时,S最大,此时
时,S最大,此时![]() ;
;
(3)由题知,![]() ,
,
当![]() 时,
时,![]() ,
,
∴点C与点M关于对称轴对称,
∴![]() ;
;
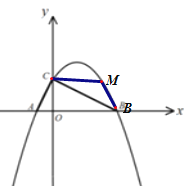
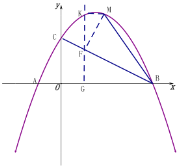
当![]() 时,过M作
时,过M作![]() 于F,过F作y轴的平行线,交x轴于G,交过M平行于x轴的直线于K,
于F,过F作y轴的平行线,交x轴于G,交过M平行于x轴的直线于K,
∵∠![]() ,BFM=∠BGF,
,BFM=∠BGF,
∴△MFK∽△FGB,
同理可证:![]() ,
,
∴![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,
,
∴![]() ,
,
∴![]() ,代入
,代入![]() ,
,
解得
![]() ,或
,或![]() (舍去),
(舍去),
∴![]() ,
,
故![]() 或
或![]() .
.

 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案【题目】庐阳春风体育运动品商店从厂家购进甲,乙两种T恤共400件,其每件的售价与进货量![]() (件)之间的关系及成本如下表所示:
(件)之间的关系及成本如下表所示:
T恤 | 每件的售价/元 | 每件的成本/元 |
甲 |
| 50 |
乙 |
| 60 |
|
(1)当甲种T恤进货250件时,求两种T恤全部售完的利润是多少元;
(2)若所有的T恤都能售完,求该商店获得的总利润![]() (元)与乙种T恤的进货量
(元)与乙种T恤的进货量![]() (件)之间的函数关系式;
(件)之间的函数关系式;
(3)在(2)的条件下,已知两种T恤进货量都不低于100件,且所进的T恤全部售完,该商店如何安排进货才能使获得的利润最大?
【题目】某塑料厂生产一种家用塑料制品,它的成本是![]() 元
元![]() 件,售价是
件,售价是![]() 元
元![]() 件,年销售量为
件,年销售量为![]() 万件.为了获得更好的效益,厂家准备拿出一定的资金做广告.根据测算,若每年投入广告费
万件.为了获得更好的效益,厂家准备拿出一定的资金做广告.根据测算,若每年投入广告费![]() 万元,产品的年销售量将是原销售量的
万元,产品的年销售量将是原销售量的![]() 倍,且
倍,且![]() 与
与![]() 之间满足
之间满足![]() ,具体数量如下表:
,具体数量如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)求![]() 与
与![]() 的函数关系式(不要求写出自变量的取值范围);
的函数关系式(不要求写出自变量的取值范围);
(2)如果把利润看作是销售总额减去成本费用和广告费用,试求出年利润![]() (万元)与广告费用
(万元)与广告费用![]() (万元)的函数关系式,并计算每年投入的广告费是多少万元时,所获得的利润最大?
(万元)的函数关系式,并计算每年投入的广告费是多少万元时,所获得的利润最大?
(3)如果厂家希望年利润![]() (万元)不低于
(万元)不低于![]() 万元,请你帮助厂家确定广告费
万元,请你帮助厂家确定广告费![]() 的范围.
的范围.