题目内容
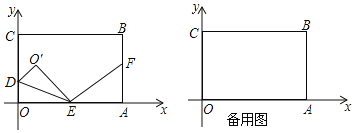
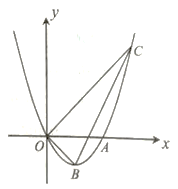
【题目】如图，在Rt△ABC中，∠C＝90°，AC＝6，AD∥BC，DE与AB交于点F，已知AD＝4，DF＝2EF，sin∠DAB＝
，则线段DE＝_____．
【答案】2
【解析】
作DG⊥BC于G，则DG＝AC＝6，CG＝AD＝4，由平行线得出△ADF∽△BEF，得出
＝
＝2，求出BE＝
AD＝2，由平行线的性质和三角函数定义求出AB＝
C＝10，由勾股定理得出BC＝8，求出EG＝BC﹣BE﹣CG＝2，再由勾股定理即可得出答案．
解：作DG⊥BC于G，则DG＝AC＝6，CG＝AD＝4，
∵AD∥BC，
∴△ADF∽△BEF，
∴＝＝2，
∴BE＝AD＝2，
∵AD∥BC，
∴∠ABC＝∠DAB，
∵∠C＝90°，
∴sin∠ABC＝
＝sin∠DAB＝
，
∴AB＝AC＝×6＝10，
∴BC＝
＝8，
∴EG＝BC﹣BE﹣CG＝8﹣2﹣4＝2，
∴DE＝
＝
＝2；
故答案为：2．
练习册系列答案
相关题目
【题目】某塑料厂生产一种家用塑料制品，它的成本是
元
件，售价是
元件，年销售量为
万件．为了获得更好的效益，厂家准备拿出一定的资金做广告．根据测算，若每年投入广告费
万元，产品的年销售量将是原销售量的
倍，且与之间满足
，具体数量如下表：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
（1）求与的函数关系式（不要求写出自变量的取值范围）；
（2）如果把利润看作是销售总额减去成本费用和广告费用，试求出年利润
（万元）与广告费用（万元）的函数关系式，并计算每年投入的广告费是多少万元时，所获得的利润最大？
（3）如果厂家希望年利润（万元）不低于
万元，请你帮助厂家确定广告费的范围．
