题目内容
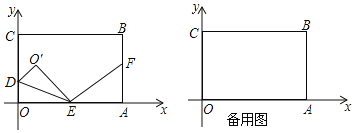
【题目】如图![]() ,已知
,已知![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 是
是![]() 上五点,
上五点,![]() 的直径
的直径![]() ,
,![]() .
.![]() 为
为![]() 的中点,延长
的中点,延长![]() 到点
到点![]() .使
.使![]() ,连接
,连接![]() .
.
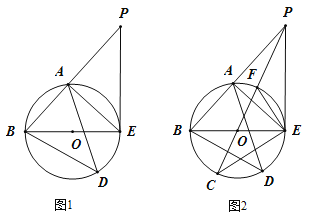
(1)求线段![]() 的长;
的长;
(2)求证:直线![]() 是
是![]() 的切线.
的切线.
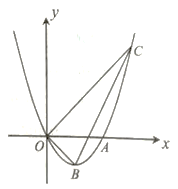
(3)如图![]() ,连
,连![]() 交
交![]() 于点
于点![]() ,延长交PO交
,延长交PO交![]() 于另一点
于另一点![]() ,连
,连![]() 、
、![]() ,求
,求![]() 的值.
的值.
【答案】(1)3;(2)见解析;(3)![]()
【解析】
(1)连接DE,如图,利用圆周角定理得∠DEB=60°,再根据圆周角定理得到∠BDE=90°,然后根据含30度的直角三角形三边的关系计算BD的长;
(2)根据圆周角定理得到∠BAE=90°,而A为![]() 的中点,则∠ABE=45°,再根据等腰三角形的判定方法,利用BA=AP得到△BEP为等腰直角三角形,所以∠PEB=90°,然后根据切线的判定定理得到结论;
的中点,则∠ABE=45°,再根据等腰三角形的判定方法,利用BA=AP得到△BEP为等腰直角三角形,所以∠PEB=90°,然后根据切线的判定定理得到结论;
(3)由切线的性质得出∠PEF=∠PCE,则△PEF∽△PCE,由相似三角形的性质可得![]() ,在Rt△PEO中,利用勾股定理求出PO的长,即可得出
,在Rt△PEO中,利用勾股定理求出PO的长,即可得出![]() 的值,再根据圆周角定理得到∠CEF=90°,即可得出
的值,再根据圆周角定理得到∠CEF=90°,即可得出![]() 的值.
的值.
(1)解:连接DE,如图,
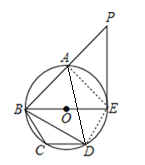
∵∠BAD =60°,
∴∠DEB=∠BAD =60°,
∵BE为直径,
∴∠BDE=90°,
在Rt△BDE中,DE=![]() BE=
BE=![]() ×2
×2![]() =
=![]() ,
,
BD=![]() DE=
DE=![]() ×
×![]() =3;
=3;
(2)证明: ∵BE为直径,
∴∠BAE=90°,
∴EA⊥BA,
∵A为![]() 的中点,
的中点,
∴∠ABE=45°,
∵BA=AP,
而EA⊥BA,
∴△BEP为等腰直角三角形,
∴∠PEB=90°,
∴PE⊥BE,
∴直线PE是⊙O的切线;
(3)解:由(2)得△BEP为等腰直角三角形,
∴PE=BE=2![]() ,
,
∵BE为直径,
∴OE=OC=![]() ,
,
∵直线PE是⊙O的切线,CF为直径,
∴∠PEF+∠OEF =∠CEO+∠OEF=90°,
∴∠PEF=∠CEO,
∵OC=OE,
∴∠PCE=∠CEO,
∴∠PEF=∠PCE,
∵∠EPF=∠CPE,
∴△PEF∽△PCE,
∴![]() ,
,
在Rt△PEO中,![]() =
=![]() ,
,
∴PC=PO+OC=![]() +
+![]() ,
,
∵CF为直径,
∴∠CEF=90°,
∴![]() =
=![]() =
=![]() .
.

【题目】某中学开展演讲比赛活动,九(1)、九(2)班根据初赛成绩各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.

(1)根据图填写下表;
平均分 (分) | 中位数 (分) | 众数(分) | 极差 | 方差 | |
九(1)班 | 85 | ______ | 85 | ______ | 70 |
九(2)班 | 85 | 80 | ______ | ______ | ______ |
(2)结合两班复赛成绩的平均数和中位数、极差、方差,分析哪个班级的复赛成绩较好?
(3)如果在每班参加复赛的选手中分别选出2人参加决赛,你认为哪个班的实力更强一些,说明理由.