题目内容
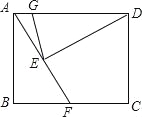
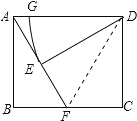
【题目】如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E.以D为圆心,DE为半径作圆弧交AD于点G,若BF=FC=1,则![]() 的长为 .
的长为 .
【答案】![]()
【解析】
试题分析:连接DF,如图所示:
∵四边形ABCD是矩形,
∴∠B=∠C=90°,AB=BC=AD=DC,AD∥BC,
∴∠EAD=∠AFB,
∵DE⊥AF,
∴∠AED=90°,
在△ADE和△FAB中,
 ,
,
∴△ADE≌△FAB(AAS),
在△DCF和△ABF中,
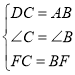 ,
,
∴△DCF≌△ABF(SAS),
∴DF=AF,
∵AF=AD,
∴DF=AF=AD,
∴△ADF是等边三角形,
∴∠DAE=60°,
∵DE⊥AF,
∴∠AED=90°,
∴∠ADE=30°,
∵△ADE≌△FAB,
∴AE=BF=1,
∴DE=![]() AE=
AE=![]() ,
,
∴![]() 的长=
的长=![]() .
.
故答案为:![]() .
.

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目