题目内容
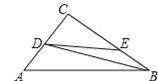
【题目】如图,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点D从点C出发,以2cm/s的速度沿折线C﹣A﹣B向点B运动,同时,点E从点B出发,以1cm/s的速度沿BC边向点C运动,设点E运动的时间为t(s)(0<t<8).
(1)求AB的长;
(2)当△BDE是直角三角形时,求t的值;
(3)设△CDE的面积为y(cm2),求y与t的函数关系式.
【答案】(1)10(2)![]() 或
或![]() (3)当0<t≤3时,y=8t﹣t2;当3<t<8时,y=
(3)当0<t≤3时,y=8t﹣t2;当3<t<8时,y=![]() t2﹣
t2﹣![]() t+
t+![]()
【解析】
试题分析:(1)直接利用勾股定理计算;
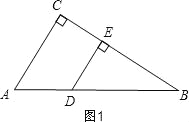
(2)当△BDE是直角三角形时,∠B不可能为直角,所以分两种情况讨论:i)图1,当∠BED=90°时;ii)图2,当∠EDB=90°时;利用相似求边,再利用同角三角函数值列等式计算求出t的值;
(3)分两种情况用三角形的面积公式求解即可.
试题解析:(1)由勾股定理得:AB=![]() =10,
=10,
(2)如图1,当∠BED=90°时,△BDE是直角三角形,
则BE=t,AC+AD=2t,
∴BD=6+10﹣2t=16﹣2t,
∵∠BED=∠C=90°,
∴DE∥AC,
∴![]() ,
,
∴![]() ,
,
∴DE=![]() t,
t,
∵sinB=![]() ,
,
∴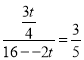 ,
,
t=![]() ;
;
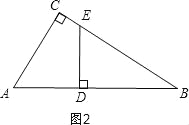
如图2,当∠EDB=90°时,△BDE是直角三角形,
则BE=t,BD=16﹣2t,
cosB=![]() ,
,
∴![]() ,
,
∴t=![]() ;
;
∴当△BDE是直角三角形时,t的值为![]() 或
或![]()
(3)当0<t≤3时,y=![]() ×2t×(8﹣t)=8t﹣t2;
×2t×(8﹣t)=8t﹣t2;
当3<t<8时,y=![]() (8﹣t)×
(8﹣t)×![]() (16﹣2t)=
(16﹣2t)=![]() t2﹣
t2﹣![]() t+
t+![]() .
.

练习册系列答案
相关题目