题目内容
【题目】请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分:
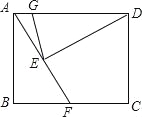
A.如图,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E、F、G、H分别为边AD、AB、BC、CD的中点,若四边形EFGH的面积12,则四边形ABCD的面积为 .
B.如图,AB、CD是两栋楼,且AB=CD=30m,两楼间距AC=24m,当太阳光与水平线的夹角为30°时,AB楼在CD楼上的影子是 m.(精确到0.1m)
【答案】A、24;B、16.1.
【解析】
试题分析:A、∵点E、F、G、H分别为边AD、AB、BC、CD的中点,
∴HG是△DBC的中位线,
∴GH∥BD,
∴△CHG∽△BDC,
∴S△CHG=![]() S△BDC,
S△BDC,
同理S△AEF=![]() S△ADB,
S△ADB,
∴S△CHG+S△AEF=![]() S△BDC+
S△BDC+![]() S△ADB=
S△ADB=![]() S四边形ABCD,
S四边形ABCD,
同理S△DEH+S△BFG=![]() S四边形ABCD,
S四边形ABCD,
∴S△CHG+S△AEF+S△DEH+S△BFG,
=![]() S四边形ABCD+
S四边形ABCD+![]() S四边形ABCD,
S四边形ABCD,
=![]() S四边形ABCD,
S四边形ABCD,
∴S四边形ABCD=2S四边形EFGH=2×12=24;
故答案为:24.
B、延长EA交CD于G,过G作GH⊥AB于H,
∵太阳光与水平线的夹角为30°,
∴∠AGH=30°,
∵BC=GH=24,
在Rt△AHG中,tan30°=![]() ,
,
∴AH=24×tan30°=24×![]() =8
=8![]() ,
,
∴CG=BH=AB﹣BH=30﹣8![]() =30﹣8×1.732≈16.1,
=30﹣8×1.732≈16.1,
故答案为:16.1.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案
相关题目